Robot weld type recognition based on improved grey wolf algorithm optimizing SVM
-
摘要:
基于双目视觉传感器的机器人移动平台建立图像采集系统,研究了一种改进的灰狼算法和最小化参数策略结合,来优化支持向量机,实现对不同焊缝类型进行识别。首先,在灰狼算法中引入佳点集理论生成初始种群,减少灰狼种群种类数,为算法全局搜索的快捷和稳定性奠定基础。然后,在分类器SVM中引入非线性收敛因子,并结合最小化参数的策略,加强最优参数的泛化能力。最后,通过基于最优参数建立的SVM模型进行焊缝类型识别试验。证明了改进算法优化的SVM模型相对于粒子群算法、遗传算法、布谷鸟算法和基本灰狼算法,在识别准确率和优化速度方面都有了较大的提升。
Abstract:An image acquisition system based on binocular visual sensors for robot mobile platforms was established, and an improved grey wolf algorithm combined with a minimization parameter strategy was studied to optimize support vector machines and achieve recognition of different weld types. Firstly, introducing the theory of the best point set into the Grey Wolf algorithm to generate an initial population, reducing the number of species in the Grey Wolf population and laying the foundation for the fast and stable global search of the algorithm. Then, a nonlinear convergence factor was introduced into the classifier SVM and combined with a strategy of minimizing parameters to enhance the generalization ability of the optimal parameters. Finally, an SVM model based on the optimal parameters was used for weld seam type recognition experiments. It is proved that the improved algorithm optimized SVM model has significantly improved recognition accuracy and optimization speed compared to particle swarm optimization, genetic algorithm, cuckoo bird algorithm, and basic grey wolf algorithm.
-
0. 前言
焊接是最为重要的制造工艺之一,高水平的焊接制造对中国工业的长期向好发展具有极大的促进作用。焊接技术作为制造业生产领域的关键环节,如何自动高效地检测出焊缝类型对焊接效果起着决定性的作用[1]。
焊缝类型识别是焊接自动化的重要一环,有助于提高焊接的质量和效率[2],其中,(Support vector machines, SVM)是一种基于监督学习的图像分类器,其分类效果优于大多数机器学习分类方法[3]。Lu等人[4]提出开发了一种结合模糊去除冗余限制玻尔兹曼机与支持向量机的模型,实现不同图像样本数据的快速高精度自动分类。葛亮等人[5]利用主成分分析提取焊缝缺陷主要特征,并导入支持向量机中进行有效识别。由于焊缝的类型具有一定的多样性,为了实现对焊缝的分类,需要提取不同类型焊缝的特征信息[6]。Zernike矩是一组正交矩,具有旋转不变性的特性[7],提取的特征有利于支持向量机识别焊缝。刘军等人[8]提出一种基于Zernike矩的亚像素方法,可快速提取焊缝中心线的直线特征。
支持向量机具有结构简单、泛化能力强等优点,但内部参数的复杂性影响分类精度[9]。为提高支持向量机的有效分类,需要对其参数进行优化。群优化算法对这类参数寻优问题有着不错的效果,使分类准确率有了极大地提升,避免了效率低下的网格搜索方式[10]。陈玉喜等人[11]基于支持向量机和粒子群算法,构建焊缝形状预测模型,实现对焊缝类型的自动检测和精确识别。佐磊等人[12]利用遗传算法改进最小二乘支持向量机提高对焊接点状态点的分类准确率。杜必强等人[13]采用粒子群算法优化支持向量机的惩罚因子和核函数参数,有效识别焊缝缺陷。Shi 等人[14]采用灰狼算法对SVM进行阈值调整,提高分类器故障检测的有效性。常用的优化算法有粒子群算法(Particle swarm optimization, PSO)、遗传算法(Genetic algorithm, GA)、布谷鸟算法(Cuckoo search, CS)和灰狼算法(Grey wolf algorithm, GWO)等。由于灰狼算法具有参数少和局部寻优能力强等优点[15],文中结合灰狼算法和支持向量机实现焊缝类型有效分类。
为提高焊缝类型识别的准确率和速度,基于焊缝图像的特点,研究了一种改进灰狼优化算法(IGWO)与最小化参数策略优化支持向量机相结合的焊缝分类方法。首先,采用佳点集法生成初始种群,使算法的初代解空间具有高的均匀性和稳定性,避免搜索效率产生波动;其次,针对数据特点,减少灰狼种群的种类数,提高了算法运行效率;引入非线性收敛因子并结合最小化参数的策略,增强最优参数的泛化能力;最后,通过基于最优参数建立的支持向量机分类器识别焊缝类型。
1. 试验平台检测系统
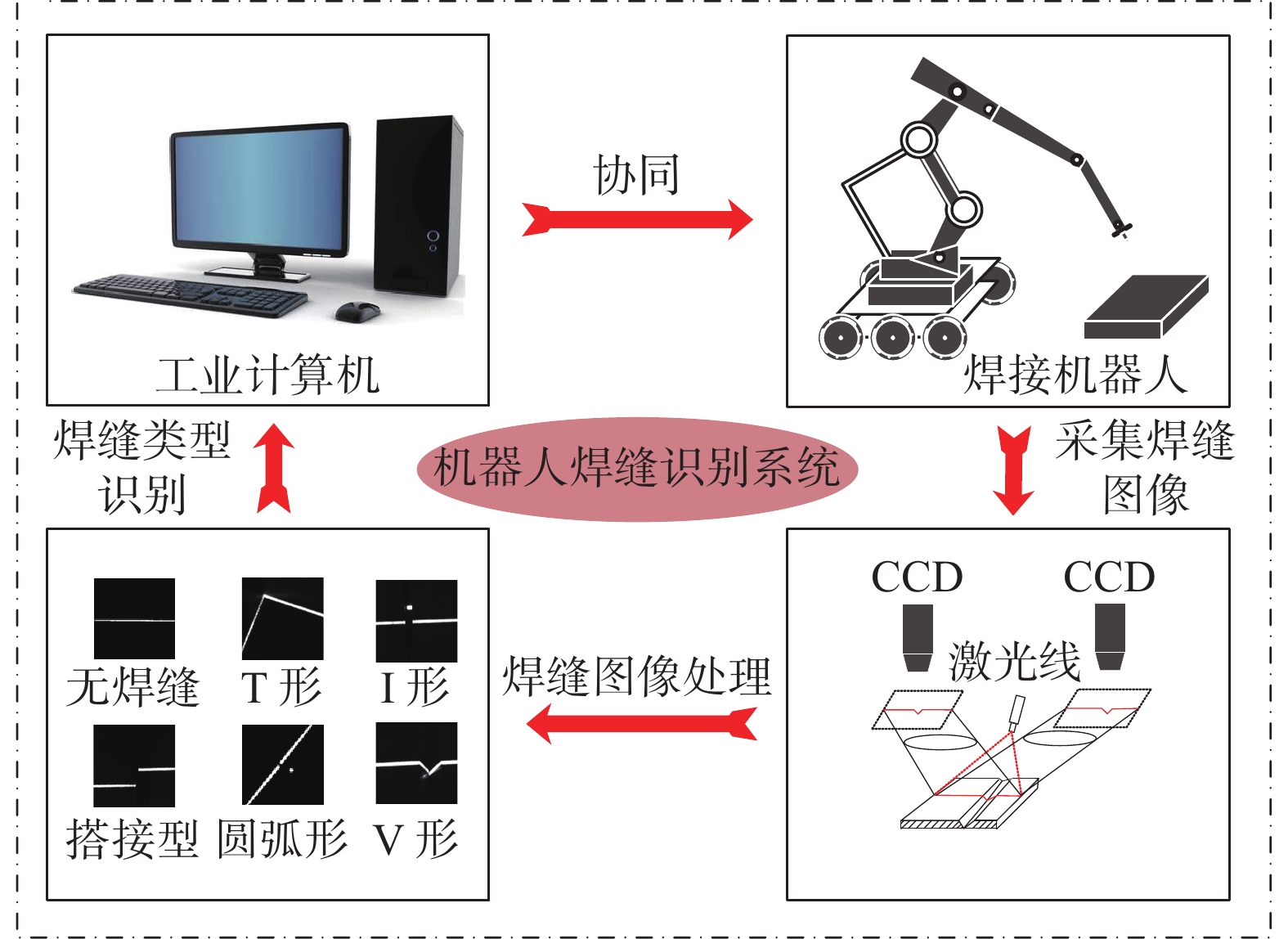
基于双目视觉的机器人焊缝识别系统如图1所示,整个系统主要包括:工业计算机、焊接机器人、1个激光视觉传感器。其中,激光视觉传感器搭载在焊接机器人上,协同工业计算机采集焊缝图像,对焊缝类型进行智能识别。激光视觉传感器由2个相同的CCD相机和1个一字线激光器构成,一字线激光器安装在2个CCD相机的中下方。其中,双目视觉可以实现三维立体空间转化为二维平面空间的一个过程。通过同一时刻不同角度拍摄,可以得到1张更具有深度和颜色信息的清晰焊缝图像,较于单目视觉,双目视觉获取的信息更丰富,有效提高了焊缝类型检测的准确率。
2. 焊缝特征理论建模
2.1 Zernike矩
Zernike矩[16]具有较小冗余性和相关性的优点,且可以构造到任意高阶,故一般用模$|{Z_{\rm pq}}|$作为图像的形状特征向量。目标图像的整体形状特征可由低阶特征向量描述,而细节则可通过高阶特征向量反映。
设定二维离散图像的灰度分布函数为$f(x,y)$,其$(p + q)$阶矩为
$$ {m_{\rm pq}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {{x^p}{y^p}} f(x,y) ,\;\;p,q = 0,1,2\cdots} $$ (1) $(p + q)$的中心矩表示为
$$ {\mu _{\rm pq}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {(x - {x_0}} } {)^p}{(y - {y_0})^q}f(x,y),\;\;p,q = 0,1,2\cdots $$ (2) $\bar x$和$\bar y$代表着图像的重心,其定义为
$$ \bar x = \dfrac{{{m_{10}}}}{{{m_{00}}}},\;\;\bar y = \dfrac{{{m_{01}}}}{{{m_{00}}}} $$ (3) 对中心矩归一化得
$$ {n_{\rm pq}} = \dfrac{{{\mu _{\rm pq}}}}{{{\mu _{00}^r}}}{\kern 1pt} $$ (4) 式中:$ r = \dfrac{{p + q + 2}}{2};\;\;p + q = 2,3,\cdots $。
将目标质心移到图像中心,则平移后的图像为
$$ {f_1}(x,y) = f(x - \bar x,y - \bar y) $$ (5) 对平移后图像进行尺度变换,此时图像可表示为
$$ g(x,y) = f\left(\dfrac{{x - \bar x}}{\alpha },\dfrac{{y - \bar y}}{\alpha }\right) $$ (6) 式中:α为尺度因子。
根据Zernike多项式的正交完备性,在单位圆内将图像$f(x,y)$展开为
$$ f(x,y){\text{ = }}\sum\limits_{p = 0}^\infty {\sum\limits_{q = 0}^\infty {{Z_{\rm pq}}{V_{\rm pq}}(\rho ,\theta )} } $$ (7) 式中:${V_{\rm pq}}(\rho ,\theta )$为Zernike多项式;${Z_{\rm pq}}$为Zernike矩。
$$ {Z_{\rm pq}}{\text{ = }}\dfrac{{p + 1}}{\text{π} }\iint\limits_{{x^2} + {y^2} \leqslant 1} {f(x,y)V_{\rm pq}^*(\rho ,\theta ){\rm{d}}x{\rm{d}}y} $$ (8) 变为累加形式就可以应用于离散的数字图像。
$$ {Z_{\rm pq}} = \dfrac{{p + 1}}{\text{π} }\sum\limits_x {\sum\limits_y {f(x,y)V_{\rm pq}^*(\rho ,\theta ){\text{ }}} } ,{\text{ }}{x^2} + {y^2} \leqslant 1 $$ (9) 2.2 支持向量机
SVM分类器是通过几何间隔最大化来寻找最佳的分割平面,进一步实现对未知样本数据的分类。假设导入SVM分类器的样本数据集为S,即
$$ S = \left\{ {({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_{\rm{n}}},{y_{\rm{n}}})} \right\},{x_i} \in {R^n},{y_i} \in \left\{ { - 1, + 1} \right\} $$ (10) 式中:i=1, 2, 3, ···, n;${x_i}$为特征向量;${y_i}$为${x_i}$所对应的类型。
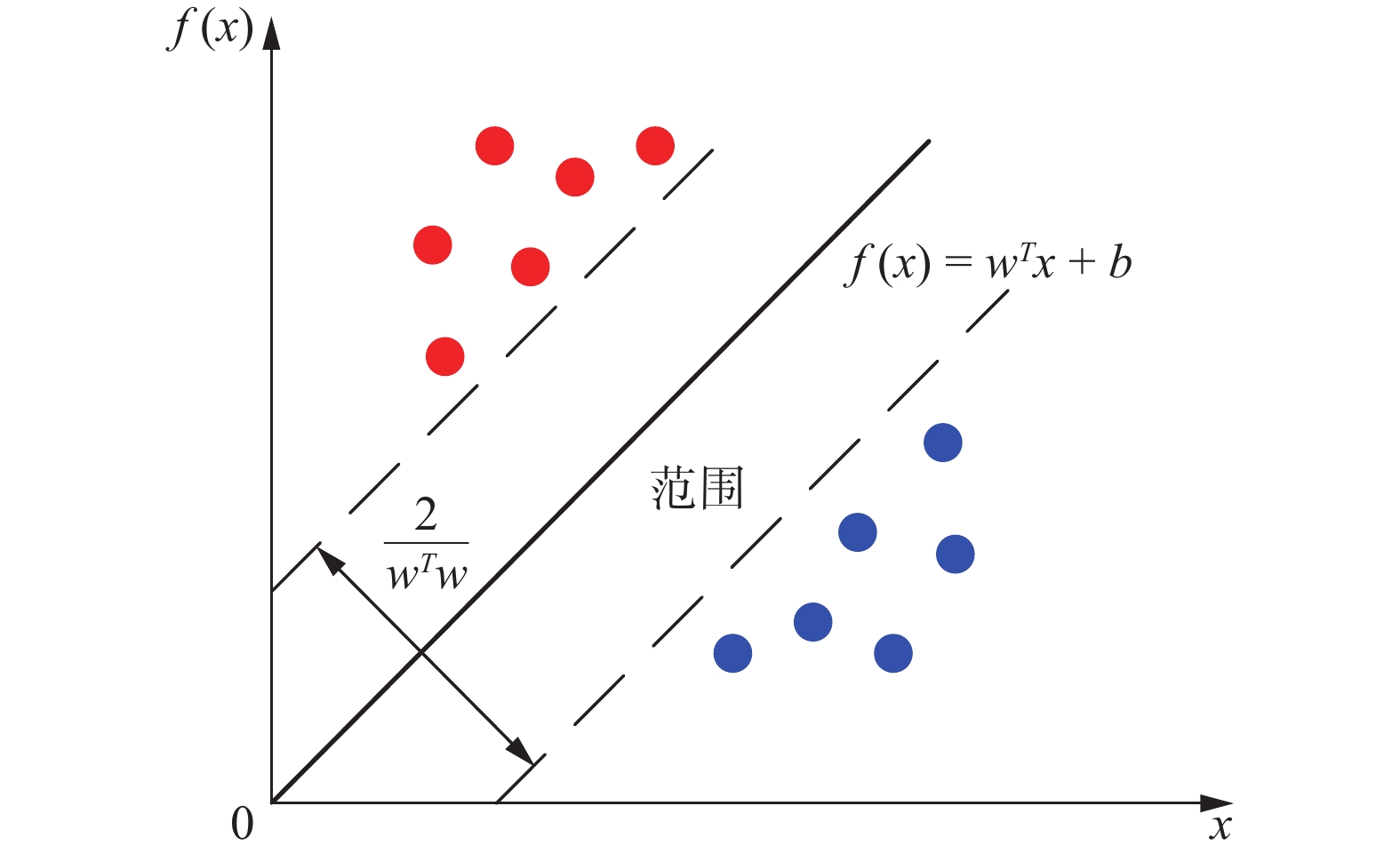
分离所有不同类型样本的超平面方程为
$$ f(x) = {w^T}x + b $$ (11) 式中:w是超平面上的m维法向量;b为截距。几何示意图如图2所示。
引入非负松弛变量$ {\xi _i} $,将分类问题转变成优化问题。
$$ \min \dfrac{1}{2}{w^T}w{\text{ + }}C\sum\limits_{i = 1}^l {{\xi _i}} $$ (12) 其约束条件为
$$ {y_i}({w^T}{x_i} + b) \geqslant 1 - {\xi _i},\;\;{\xi _i} \geqslant 0,\;\;i = 1, \cdots ,n $$ (13) 式中:C>0为惩罚因子。
通过拉格朗日函数把式(12)和式(13)转化为对偶问题,引入核函数,即
$$ \left\{ \begin{aligned} &\max - \dfrac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\alpha _i}} } {\alpha _j}{y_i}{y_j}K({x_i},x) + \sum\limits_{i = 1}^n {{\alpha _i}} \\ & \sum\limits_{i = 1}^n {{\alpha _i}} {y_i}{\text{ = }}0,\;\;C \geqslant 0,\;\;{\alpha _i} \geqslant 0 \\ \end{aligned} \right. $$ (14) 式中:${\alpha _i}$,${\alpha _j}$均为拉格朗日系数;n为样本个数。
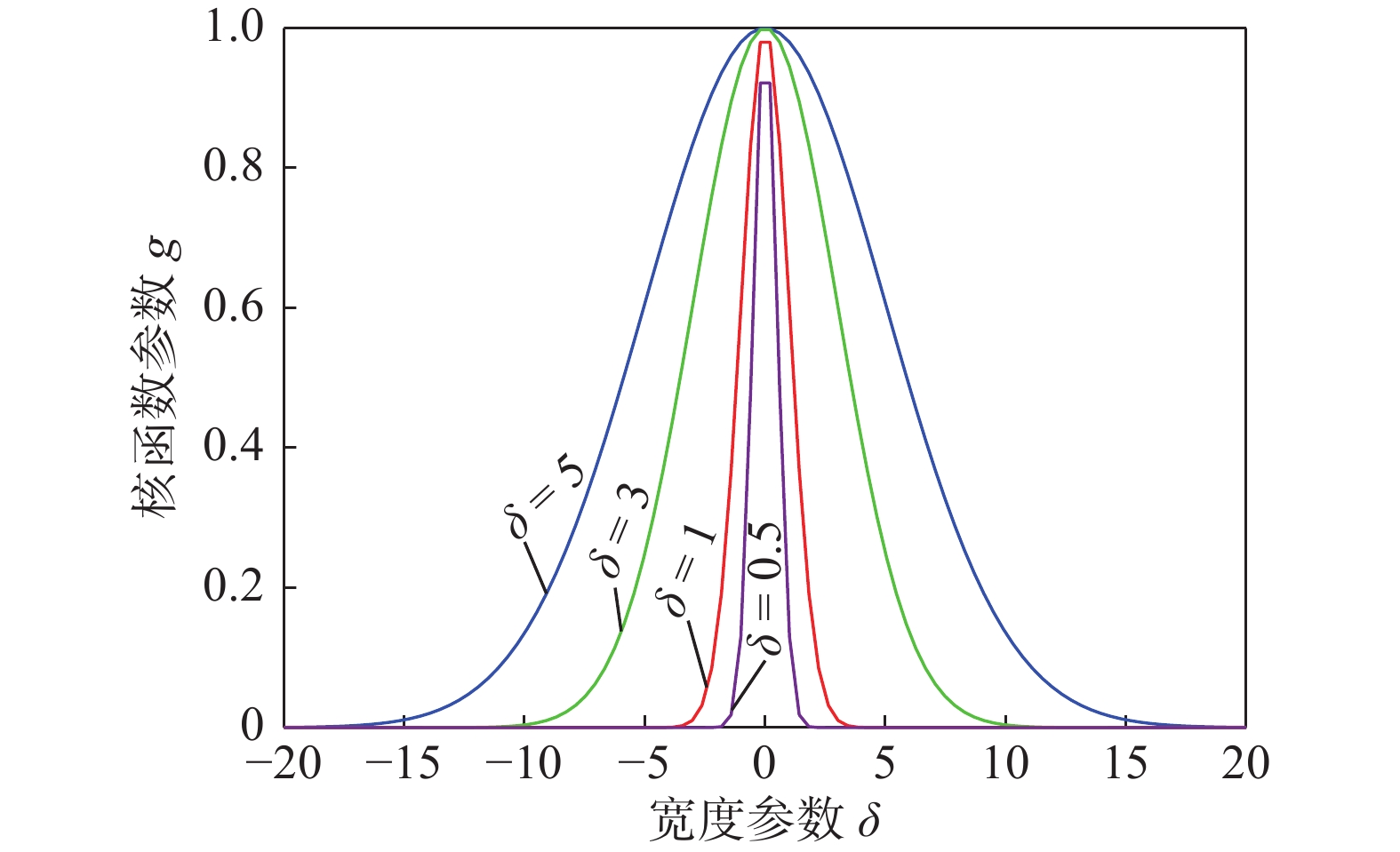
在SVM中,惩罚因子C与核函数参数g均影响着分类器的分类精度及稳定性。为有利于参数优化,选择高斯径向基核函数,如图3所示。
使用径向基核函数构造的SVM分类器可表示为
$$ K({x_i},x) = \exp \left( - \dfrac{{\left\| {{x_i} - } \right.{{\left. x \right\|}^2}}}{{2{\delta ^2}}}\right) $$ (15) 最终,超平面的求解公式为
$$ f(x) = {\rm sgn} \left(\sum\limits_{i = 1}^n {{\alpha _i}{y_i}K({x_i},x) + b} \right) $$ (16) 令$g = {1 \mathord{\left/ {\vphantom {1 {2{\delta ^2}}}} \right. } {2{\delta ^2}}}$,宽度参数δ控制了径向基核函数式(15)作用范围,以控制分类器的泛化能力。δ越小,g值过大,高斯分布变窄会造成过训练现象,则样本分类效果变差,使交叉验证的训练准确率变低,从而测试准确率不高;δ越大,g值过小,高斯分布变宽,无法在训练集上收获较高准确率,影响测试集的分类精确性。
2.3 灰狼算法
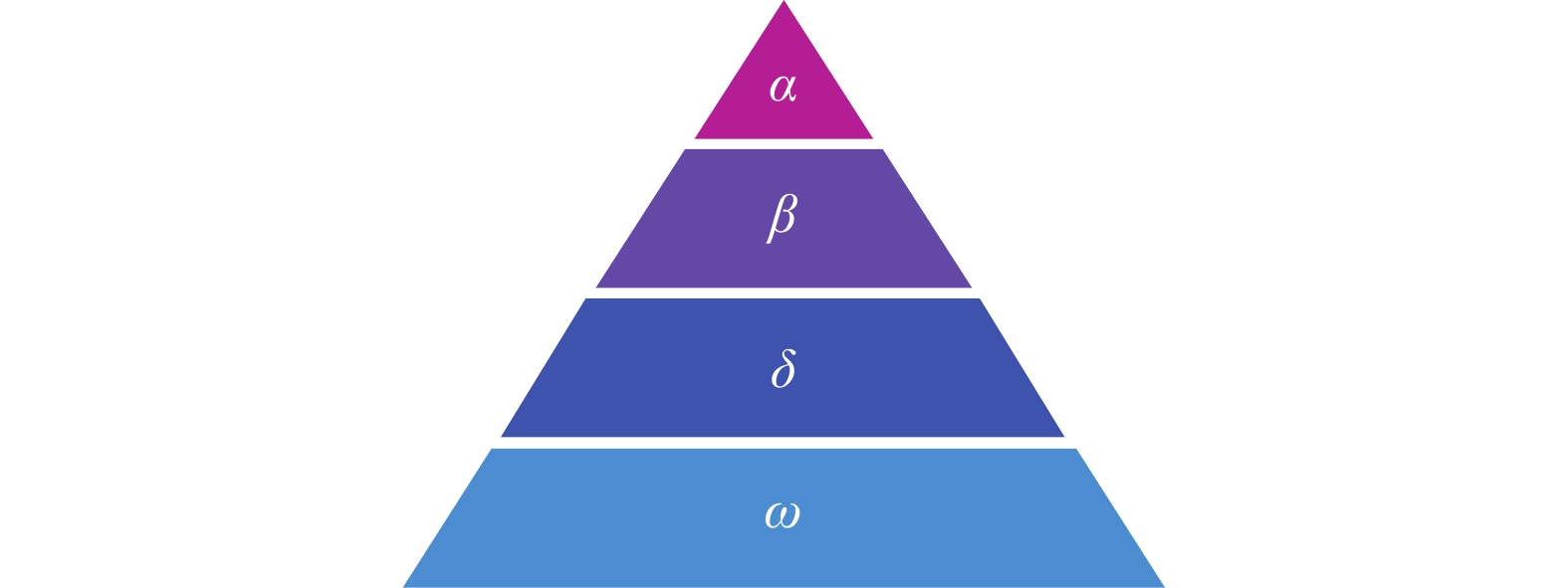
灰狼算法是一种基于狼群捕食行动的智能寻优算法。如图4所示,金字塔顶层为种群中的头狼,称为α,是狼群的主要管理者。金字塔第2层狼为β,是α的协助者,补充α空缺时的位置,具有协调反馈的作用,对其余成员具有支配权。金字塔第3层狼为δ,δ听从α及β的指令,可以指挥其他底层个体。金字塔最底层为ω狼,数量最多。
在追捕猎物的过程中,灰狼首先要确定与猎物之间的距离,完成对猎物的包围,表达式为
$$ D = \left| {E{X_{\rm{p}}}(t) - X(t)} \right| $$ (17) $$ c = 2{r_1} $$ (18) 式中:Xp表示猎物的位置;X(t)表示在t代时灰狼个体的位置;常数c为摆动因子;r1为[0,1]的随机数。
同时,更新灰狼的位置,为
$$ X(t + 1) = {X_{\rm{p}}} - AD $$ (19) $$ A = 2a{r_2} - a $$ (20) 式中:A为系数因子;r2为[0,1]的随机数;a为收敛因子,其计算式为
$$ a = 2 - 2\dfrac{t}{{{T_{\max }}}} $$ (21) 式中:${T_{\max }}$是最大迭代次数。
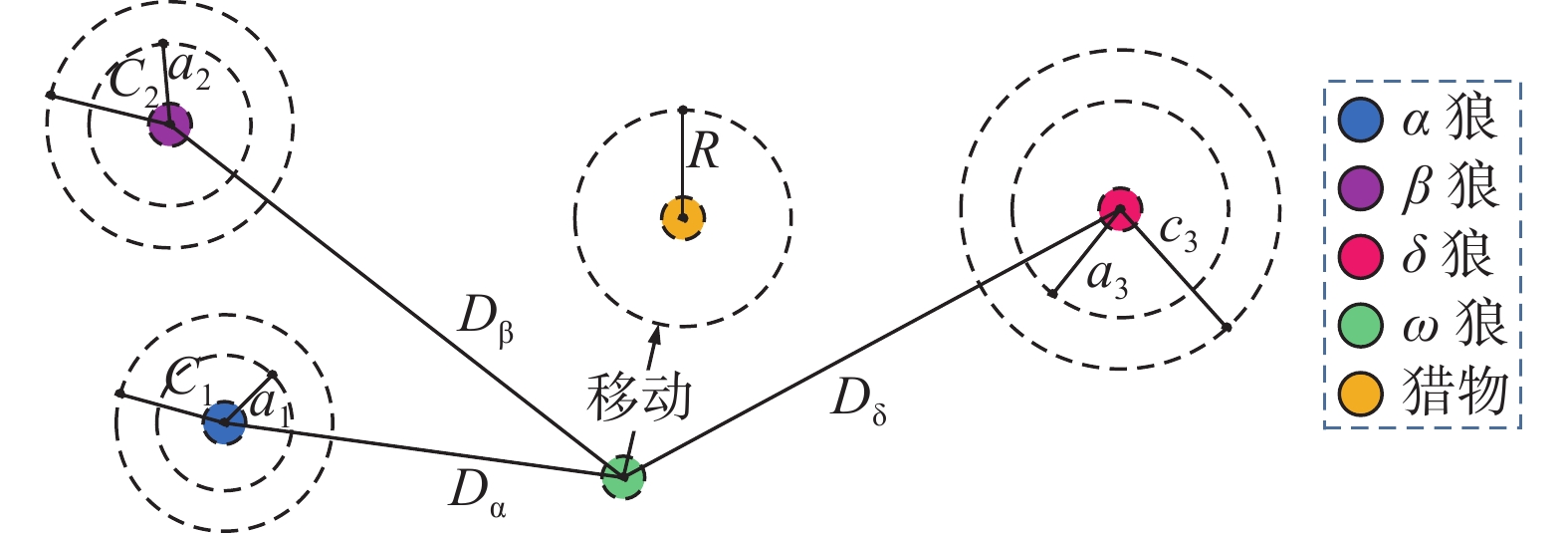
如图5所示,α,β,δ跟踪猎物方位的行为可由下式进行描述,为
$$ \left\{ {\begin{aligned} {{D_{\text α} } = \left| {{E_1}{X_{\text α} }(t) - X(t)} \right|} \\ {{D_{\text β} } = \left| {{E_2}{X_{\text β} }(t) - X(t)} \right|} \\ {{D_{\text δ} } = \left| {{E_3}{X_{\text δ} }(t) - X(t)} \right|} \end{aligned}} \right. $$ (22) $$ \left\{ {\begin{aligned} {{X_1} = {X_{\text α} } - {A_1}{D_{\text α} }} \\ {{X_2} = {X_{\text β} } - {A_2}{D_{\text β} }} \\ {{X_3} = {X_{\text δ} } - {A_3}{D_{\text δ} }} \end{aligned}} \right. $$ (23) $$ X(t + 1) = \dfrac{{{X_1} + {X_2} + {X_3}}}{3} $$ (24) 通过式(22)和式(23)确定当前候选灰狼分别与α,β,δ的距离,由式(24)确定灰狼个体向猎物移动的方向。
2.4 基于灰狼算法的改进
为提高SVM分类的有效性,基于改进的灰狼算法优化SVM分类模型,并从3个方面进行优化:①遍历性:采用佳点集理论优化种群,提高种群的遍历性,提高寻优的全局搜索能力;②收敛性:降低灰狼种群组数,提高寻优收敛性;③有效性:引入非线性收敛因子提高寻优能力。
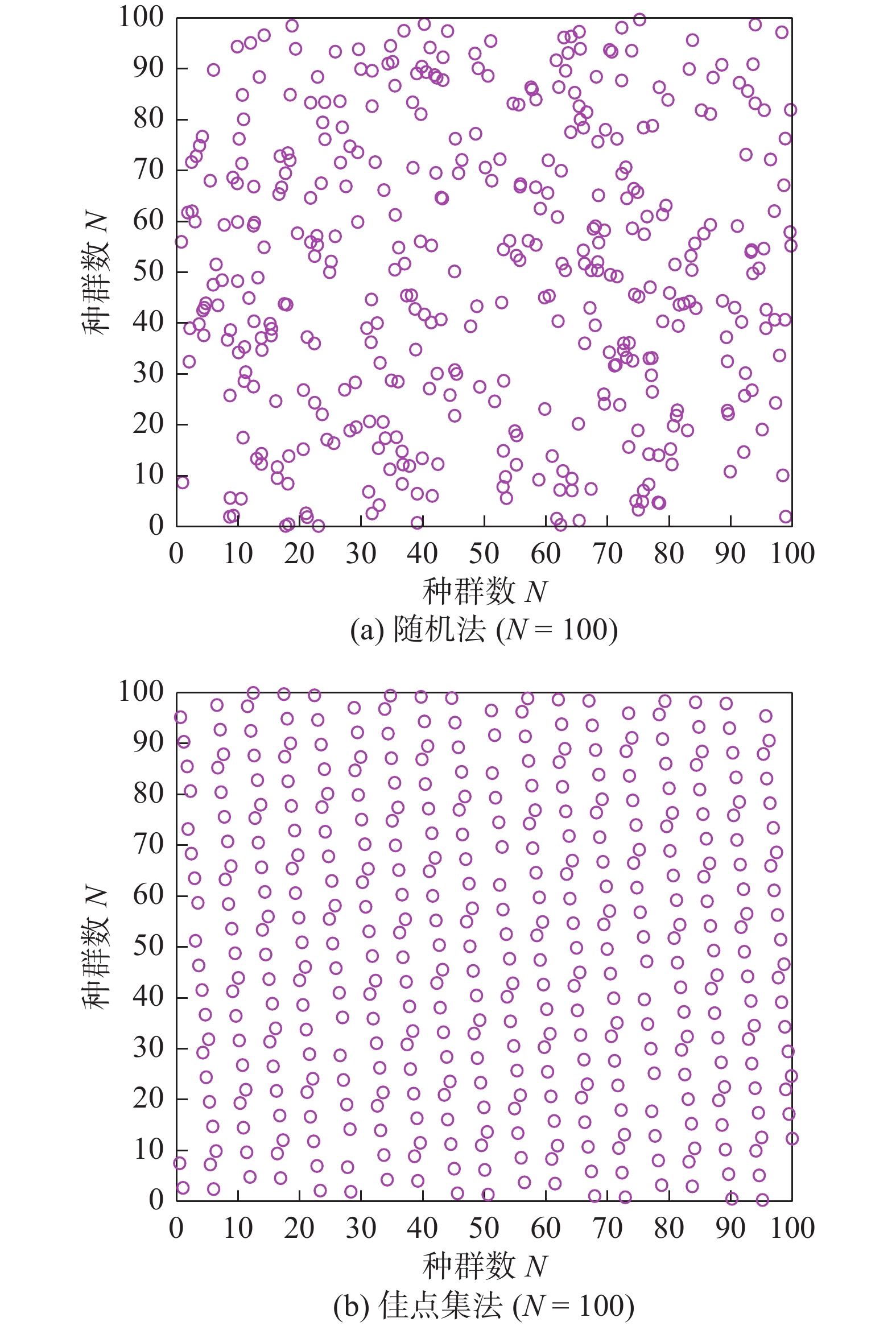
2.4.1 基于佳点集理论的种群初始化
在生成相同的种群个数时,佳点集法产生的二维初始种群较随机法更加均匀,如图6所示。在种群数为100时,随机产生的种群杂乱无章,而经过佳点集法产生的种群更加均匀有序。因此,当优化算法的求解空间采用佳点法时,使得初始种群的遍历性变得更强,且只要种群数量一定,其产生的图形是稳定不变的,达到了优化算法的全局搜索能力的目的。
设Gs是s维欧氏空间中的单位立方体,r∈Gs,所以,佳点集需满足的条件为
$$ \left\{ \begin{aligned} & {P_{\rm{n}}}(k) = \left\{ {\left(\left\{ {r_1^{(n)}*k} \right\},\left\{ {r_2^{(n)}*k} \right\}, \cdots ,\left\{ {r_{\rm{s}}^{(n)}*k} \right\}\right),\;\;1 \leqslant k \leqslant s} \right\} \\ & \varphi (n) = C(r,\varepsilon ){n^{ - 1 + \varepsilon }} \\ & r = \bigg\{ 2\cos\dfrac{{2\text{π} k}}{p},\;\;1 \leqslant k \leqslant s\bigg\} \end{aligned} \right.$$ (25) 式中:ε为任意正数;p是满足(p−3)/2≥s的最小素数。若$C(r,\varepsilon )$是只与r和ε有关的常数,则称${P_{\rm{n}}}(k)$为佳点集,r为佳点。
2.4.2 降低种群组数
降低灰狼种群组数就是将隶属度较低的狼和最小等级的狼群进行合并,即种群被分为α,β和ω 3组,达到降低算法计算复杂度和提高收敛性的目的。所以,判断个体向猎物移动的方向表达式为
$$ \left\{ {\begin{aligned} &{{D_{\text α} } = \left| {{E_1}{X_{\text α} }(t) - X(t)} \right|} \\ &{{D_{\text β} } = \left| {{E_2}{X_{\text β} }(t) - X(t)} \right|} \end{aligned}} \right. $$ (26) $$ \left\{ {\begin{aligned} & {{X_1} = {X_{\text α} } - {A_1}{D_{\text α} }} \\ & {{X_2} = {X_{\text β} } - {A_2}{D_{\text β} }} \end{aligned}} \right. $$ (27) $$ X(t + 1) = \dfrac{{{X_1} + {X_2}}}{2} $$ (28) 2.4.3 引入非线性收敛因子调制参数
基于种群的元启发式算法须在探索和开发之间取得良好的平衡,才能实现有效的全局和局部搜索。在经典的GWO算法中,自适应收敛因子a保证了算法的探索和开发,较大时可促进全局搜索,较小时可促进局部搜索。
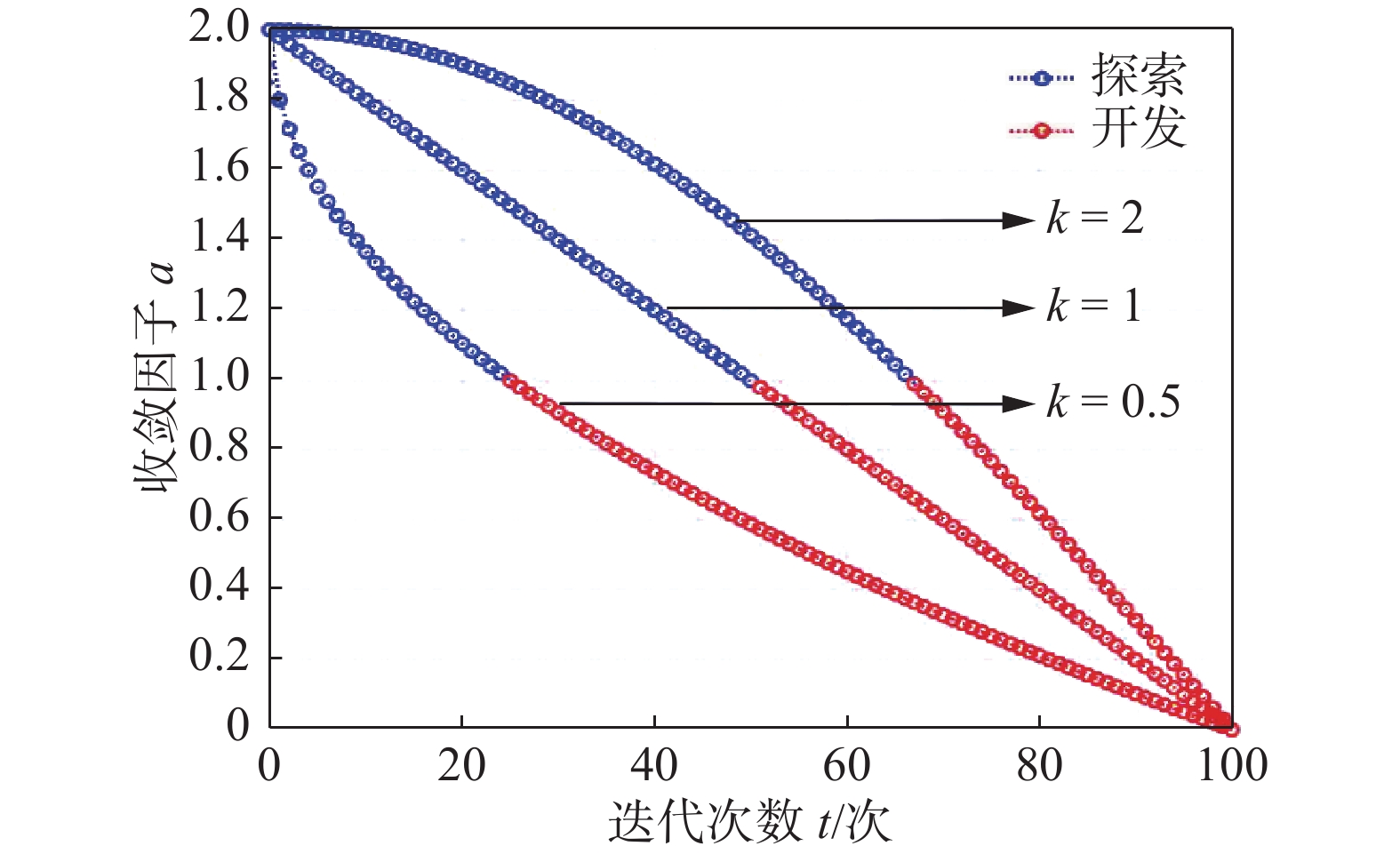
GWO算法的搜索过程是非线性的、高度复杂的,故线性递减的收敛因子a不能真实反映实际的搜索过程。而适当选择收敛因子a可以提供全局能力和局部能力之间的平衡。因此,在保证GWO算法的勘探与开发特性基本平衡的基础上,考虑采用一种新的非线性收敛方式加强对最小化g的搜索,表达式为
$$ a = 2 - 2{\left(\dfrac{t}{{{T_{\max }}}}\right)^k} $$ (29) 式中:k为调制参数;t是当前迭代次数;${T_{\max }}$是最大迭代次数;当k分别取值2,1,0.5时,随着t的递增,收敛因子a的非线性递减如图7所示。图中,探索代表研究寻找新的更好个体的搜索能力,开发代表在一个好的个体附近寻找最优个体的能力。
3. 类型识别模型
为保证焊缝特征信息提取精度,需要对焊缝图像进行模式识别。图像特征主要包括纹理、形状、颜色以及局部特征等。其中,图像的不变性特征因具有很强的准确性,而被广泛地应用于图像分类领域。基于Zernike矩的特征向量具有相关性和冗余性小的特点,有利于构建基于图像形状特征的特征向量,进行分类。
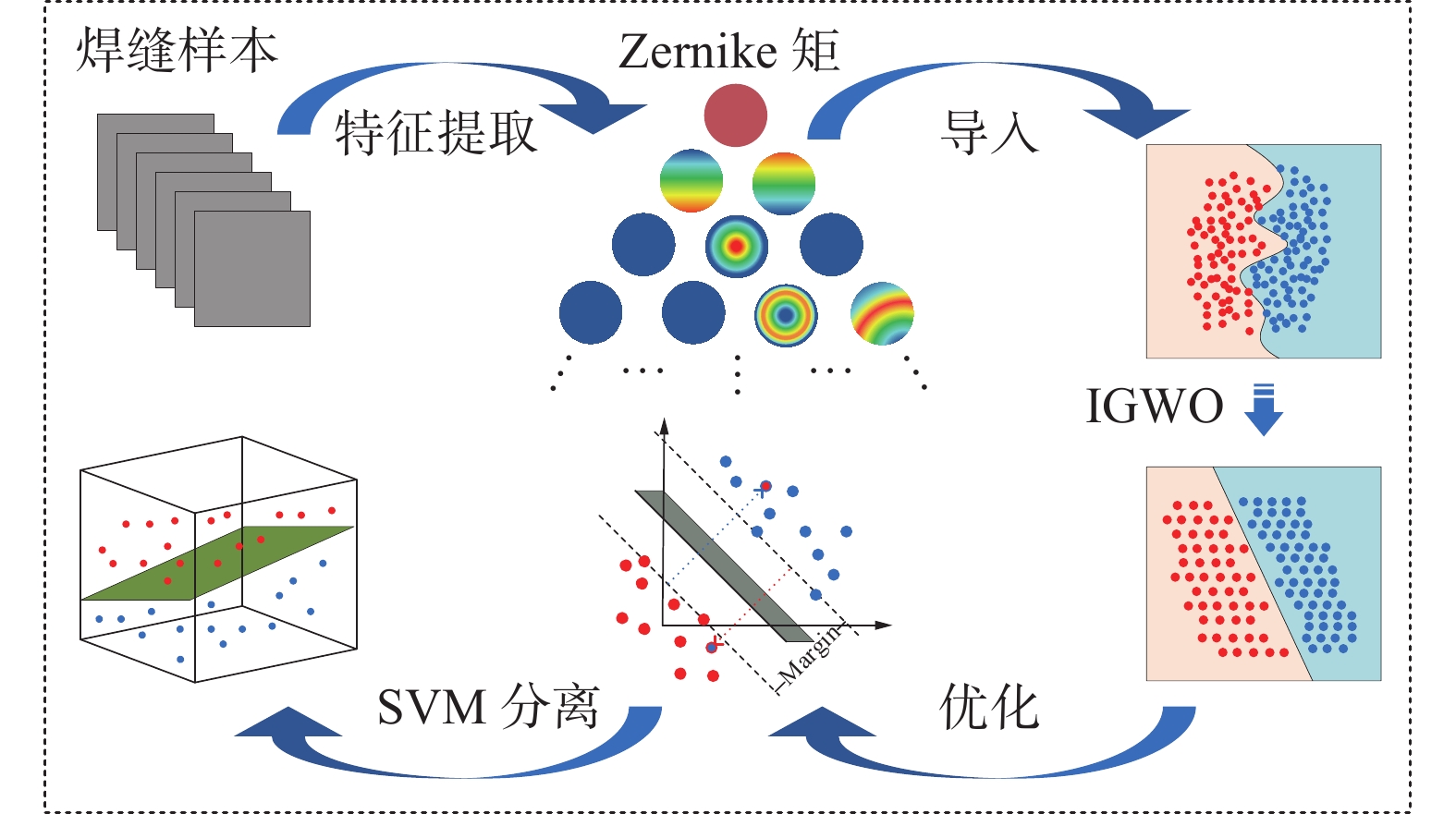
通过Zernike矩提取图像的特征,并导入改进的IGWO-SVM分类器中,构建具有特征提取和模式识别的分类模型中,对图像进行分类。图8是模式识别模型Zernike矩 + IGWO-SVM的流程图。
4. 焊缝类型识别试验
试验平台是轮式机器人双目视觉焊缝识别系统。软件操作平台为基于Windows10系统的MATLAB,Intel(R)Core(TM)i5-8300H@2.30GHz处理器,8 G内存。
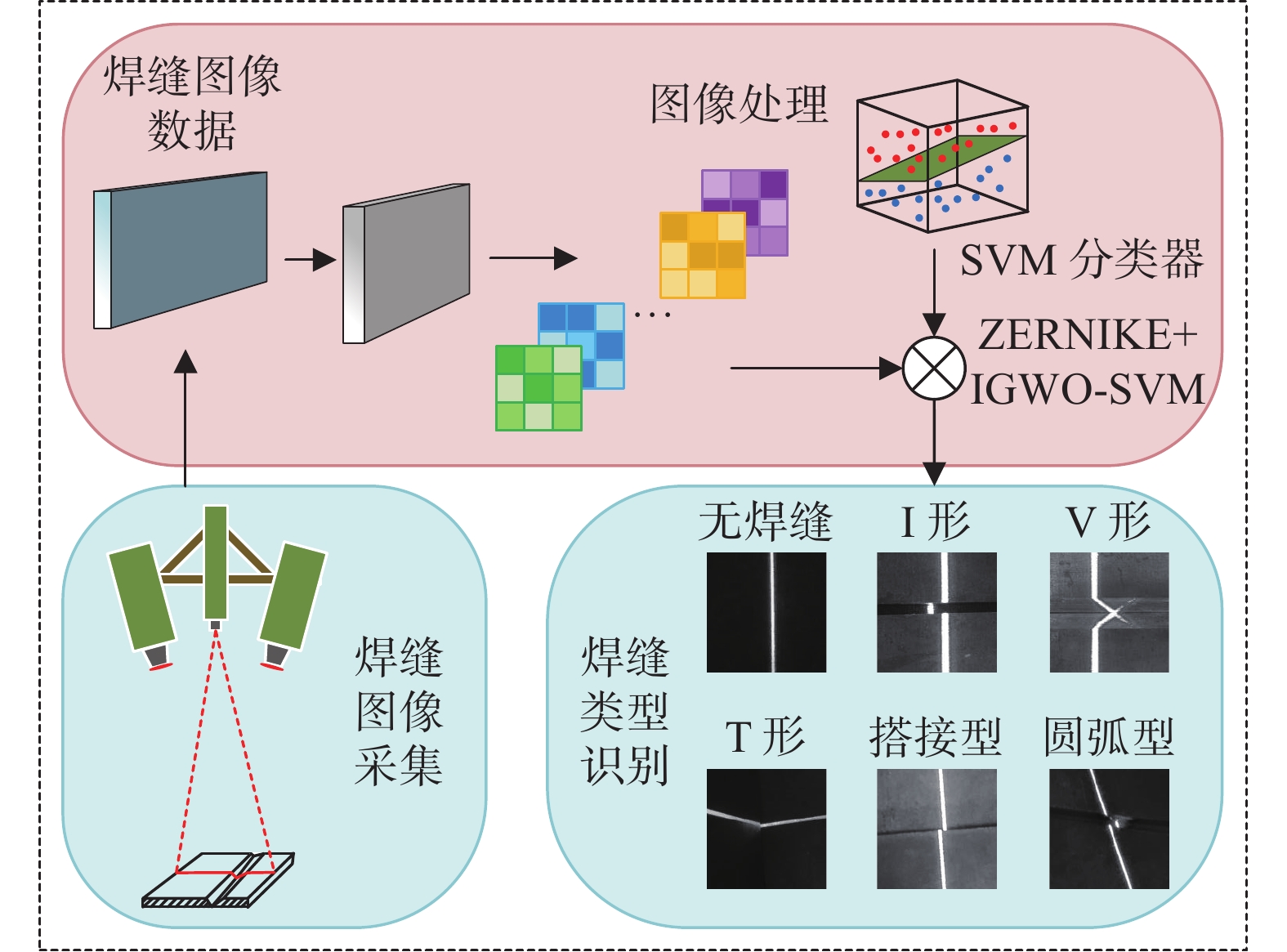
图9为试验流程,通过双目传感器采集焊缝图像,并通过PC进行图像预处理,将采集的灰度图像转为更直观的特征图像。通过Zernike不变矩进行特征提取,提炼每种焊缝类型的特征信息,并将特征信息导入IGWO-SVM分类模型中,实现焊缝类型识别。
4.1 焊缝图像预处理
采集的焊缝图像有6种类型,包括无焊缝、V形焊缝、I形焊缝、T形焊缝、搭接型焊缝和圆弧型焊缝。该试验采集每种类型焊缝图像各150幅,共计900幅。图10为6种焊缝类型的灰度图。
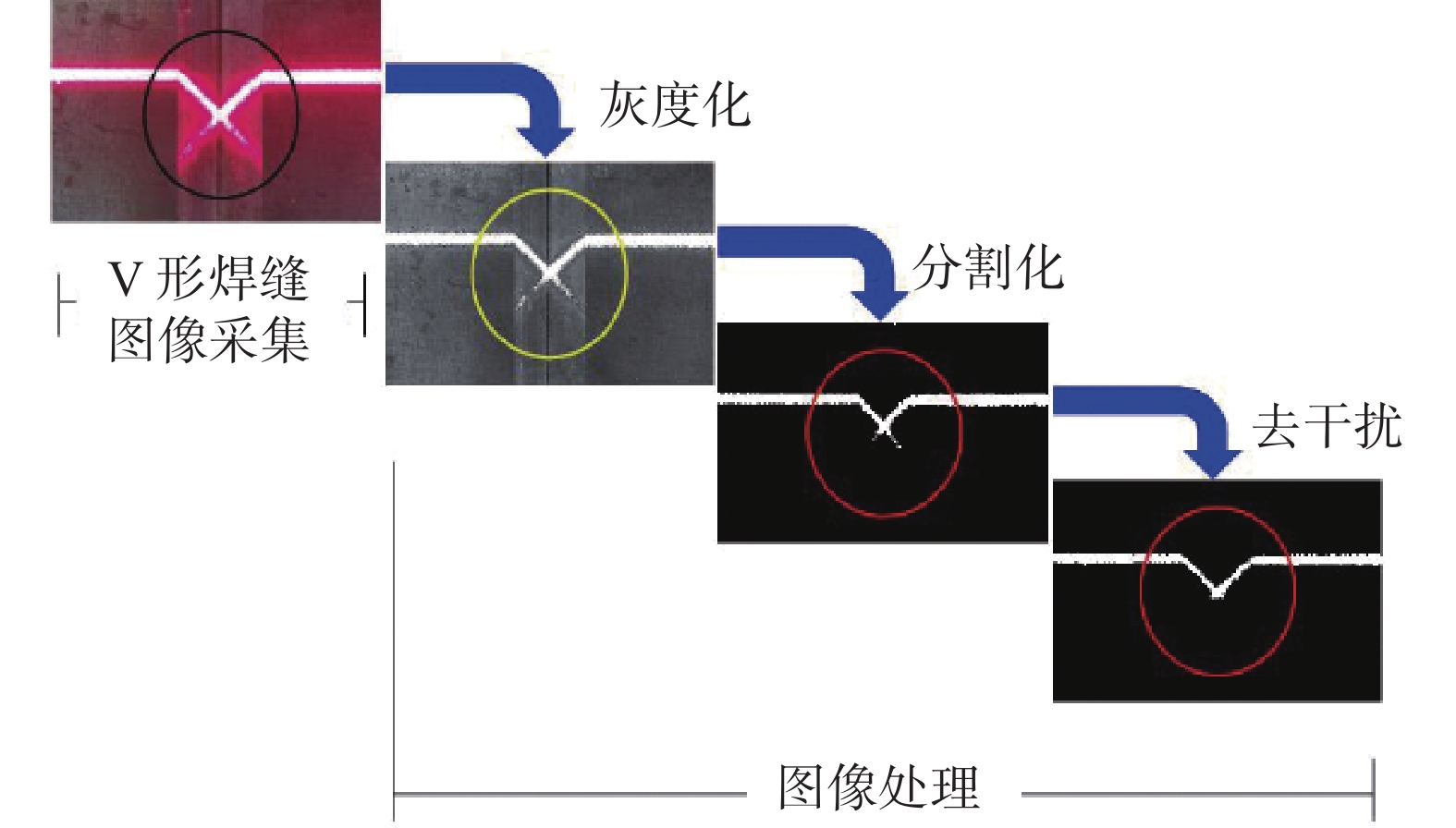
为了降低图像的内存大小,优化机器运算速度,采用MATLAB中的自带函数imresize将图片以64×64分辨率进行存储。在特征提取之前,对图像进行二值化操作,进行图像分割,将焊缝图形与背景区分开。选择3×3的中值滤波提取原始图像中焊缝的轮廓图像。当系统检测到光干扰时,需进一步去除图像干扰,以便提高特征信息的有效性和模式识别的准确度。图11为V形焊缝提取特征前的预处理过程。
4.2 Zernike + IGWO-SVM识别焊缝试验
系统利用图像预处理技术,精确提取焊缝图像的轮廓图像,并利用Zernike不变矩提取轮廓图像的特征信息,得到每种焊缝类型特征信息。表1记录了6种类型的焊缝图像Zernike不变矩特征值。
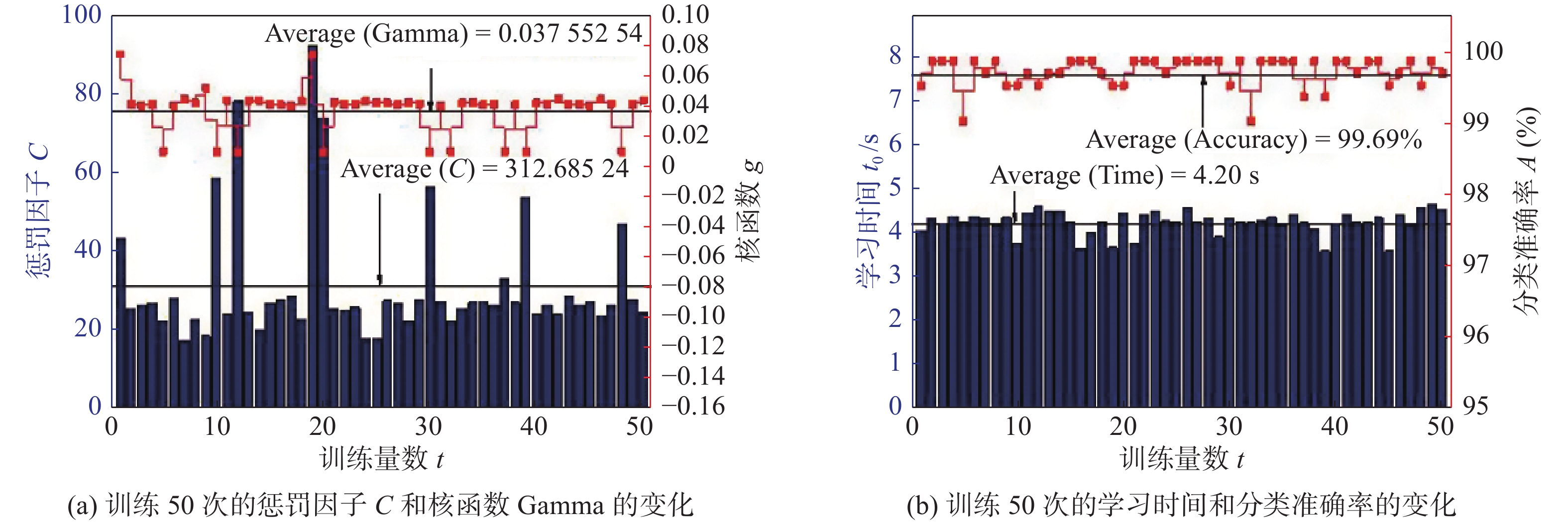
表 1 6类焊缝图像的Zernike不变矩特征向量类型 Zernike不变矩特征向量$|{Z_{\rm pq} }|$ $|{Z_{00}}|$ $|{Z_{11}}|$ $|{Z_{20}}|$ $|{Z_{22}}|$ $|{Z_{31}}{\text{|}}$ $|{Z_{33}}|$ $|{Z_{40}}|$ $|{Z_{42}}|$ $|{Z_{44}}|$ 无焊缝 6.855 2 7.804 5 2.316 6 5.857 9 6.889 4 2.960 9 5.460 2 6.920 1 0.952 2 6.802 4 7.741 9 2.284 7 5.794 5 6.817 7 2.888 6 5.393 4 6.853 3 0.875 3 6.913 5 7.884 0 2.299 6 5.926 4 6.941 3 3.002 6 5.614 1 6.982 1 0.903 7 V形 4.777 3 5.619 6 1.612 2 4.564 5 5.233 2 2.791 5 4.287 2 5.813 6 1.196 2 4.641 8 5.471 2 1.521 4 4.454 5 5.042 1 2.736 0 4.183 1 5.626 0 1.193 9 4.733 8 5.594 0 1.538 1 4.560 1 5.196 7 2.818 1 4.395 1 5.793 8 1.266 5 I形 4.381 9 5.295 4 0.929 9 4.310 1 4.487 5 2.509 0 4.256 8 5.267 7 0.853 8 4.237 5 5.124 6 0.866 0 4.172 1 4.291 1 2.428 9 4.060 9 5.052 3 0.857 2 4.128 2 4.824 2 1.602 2 3.876 0 4.791 7 2.292 3 3.642 2 5.215 3 0.791 5 T形 1.519 7 1.882 8 0.334 9 1.625 2 1.696 3 1.079 5 1.680 1 2.122 6 0.498 9 1.691 8 2.072 3 0.424 0 1.761 8 1.896 3 1.138 6 1.785 0 2.313 2 0.490 6 1.686 0 2.058 4 0.450 0 1.746 5 1.912 3 1.131 3 1.770 9 2.306 7 0.498 3 搭接型 6.462 7 7.030 5 3.345 7 5.226 3 6.979 1 2.850 2 3.669 0 6.472 2 1.408 9 6.784 0 7.015 5 4.016 6 4.680 0 7.290 9 1.861 2 3.796 5 5.879 4 0.146 2 6.839 6 7.289 3 3.992 8 5.136 7 7.800 5 2.314 3 3.637 4 6.988 8 0.696 1 圆弧型 5.567 0 6.357 5 1.444 5 4.876 9 4.778 7 2.820 0 4.196 0 4.787 5 1.620 1 5.935 7 6.632 8 2.661 1 5.041 1 6.443 7 2.810 9 4.206 9 6.379 1 1.270 0 5.856 3 6.528 5 2.671 6 4.942 9 6.390 2 2.737 9 4.123 9 6.289 4 1.236 7 将Zernike不变矩提取的特征信息导入改进的SVM中,对每种焊缝类型进行分类,构建具有特征提取和模式识别的分类模型。为检验IGWO-SVM模型的性能,分别选择粒子群算法(PSO)、遗传算法(GA)、布谷鸟算法(CS)、灰狼算法(GWO)和改进后的灰狼算法(IGWO)优化SVM。为保证寻优效率、运行时间以及收敛性方面的公平,设置表2是试验参数。图12为焊缝图像数据经Zernike + IGWO-SVM模型训练50次的性能表现图。比较不同的分类模型,具体的识别准确率及收敛代数、运行时间的平均值见表3。不同优化算法参数均值和标准差见表4,结果为训练10次的平均值。
表 2 SVM试验参数训练集样本数 测试集样本数 种群规模 N 最大迭代次数 Tmax/次 交叉验证次数 CV 惩罚因子C取值范围 核函数g取值范围 300 600 10 100 3 [0.01, 100 0] [0.001, 100] 表 3 IGWO-SVM焊缝图像识别结果算法 CV准确率
δ′(%)准确率
δ(%)收敛代数 运行时间
t′/sPSO-SVM 99.85 98.30 12.1 11.45 GA-SVM 99.96 97.86 50.4 9.80 CS-SVM 100 98.32 11.8 23.24 GWO-SVM 99.98 98.00 4.8 4.75 IGWO-SVM 99.97 99.63 4.1 4.13 表 4 参数均值和标准差对比算法 惩罚因子C 核函数参数g 平均值 标准差 平均值 标准差 PSO-SVM 222.48 222.16 0.180 4 0.154 0 GA-SVM 103.55 103.06 0.308 3 0.136 8 CS-SVM 558.19 283.66 0.220 4 0.134 2 GWO-SVM 526.00 288.86 0.264 4 0.121 0 IGWO-SVM 358.38 272.84 0.041 7 0.015 9 结果表明,IGWO-SVM模型具有极佳的分类效果、较高的收敛速度和运行速度。同时,基于文中改进措施的核函数参数g有着更小的标准差,这表明IGWO-SVM模型拥有更高的稳定性。改进后的灰狼优化算法复杂度低,求解速度快,非常适合对复杂求解过程的优化。经过优化的SVM分类器,在新的特征空间中分类更精确,训练时间更短。
5. 结论
(1) 研究了一种具有类型识别功能的分类模型IGWO-SVM,该模型基于分类器SVM结合灰狼算法进行改进,通过选择SVM最优参数值来提高焊缝的分类精度,并优化速度。
(2) 构建具有特征提取和分类功能的Zernike + IGWO-SVM模型,同时,基于双目视觉的机器人移动平台对模型进行有效性验证。结果表明,所提出的IGWO-SVM识别模型的分类准确度达到99.833%。同时,比较其他的寻优 + SVM模型。在准确率、稳定性、收敛速度以及运行时间方面,IGWO-SVM明显优于粒子群算法、遗传算法、布谷鸟算法和基本灰狼算法优化的支持向量机分类模型。
-
表 1 6类焊缝图像的Zernike不变矩特征向量
类型 Zernike不变矩特征向量$|{Z_{\rm pq} }|$ $|{Z_{00}}|$ $|{Z_{11}}|$ $|{Z_{20}}|$ $|{Z_{22}}|$ $|{Z_{31}}{\text{|}}$ $|{Z_{33}}|$ $|{Z_{40}}|$ $|{Z_{42}}|$ $|{Z_{44}}|$ 无焊缝 6.855 2 7.804 5 2.316 6 5.857 9 6.889 4 2.960 9 5.460 2 6.920 1 0.952 2 6.802 4 7.741 9 2.284 7 5.794 5 6.817 7 2.888 6 5.393 4 6.853 3 0.875 3 6.913 5 7.884 0 2.299 6 5.926 4 6.941 3 3.002 6 5.614 1 6.982 1 0.903 7 V形 4.777 3 5.619 6 1.612 2 4.564 5 5.233 2 2.791 5 4.287 2 5.813 6 1.196 2 4.641 8 5.471 2 1.521 4 4.454 5 5.042 1 2.736 0 4.183 1 5.626 0 1.193 9 4.733 8 5.594 0 1.538 1 4.560 1 5.196 7 2.818 1 4.395 1 5.793 8 1.266 5 I形 4.381 9 5.295 4 0.929 9 4.310 1 4.487 5 2.509 0 4.256 8 5.267 7 0.853 8 4.237 5 5.124 6 0.866 0 4.172 1 4.291 1 2.428 9 4.060 9 5.052 3 0.857 2 4.128 2 4.824 2 1.602 2 3.876 0 4.791 7 2.292 3 3.642 2 5.215 3 0.791 5 T形 1.519 7 1.882 8 0.334 9 1.625 2 1.696 3 1.079 5 1.680 1 2.122 6 0.498 9 1.691 8 2.072 3 0.424 0 1.761 8 1.896 3 1.138 6 1.785 0 2.313 2 0.490 6 1.686 0 2.058 4 0.450 0 1.746 5 1.912 3 1.131 3 1.770 9 2.306 7 0.498 3 搭接型 6.462 7 7.030 5 3.345 7 5.226 3 6.979 1 2.850 2 3.669 0 6.472 2 1.408 9 6.784 0 7.015 5 4.016 6 4.680 0 7.290 9 1.861 2 3.796 5 5.879 4 0.146 2 6.839 6 7.289 3 3.992 8 5.136 7 7.800 5 2.314 3 3.637 4 6.988 8 0.696 1 圆弧型 5.567 0 6.357 5 1.444 5 4.876 9 4.778 7 2.820 0 4.196 0 4.787 5 1.620 1 5.935 7 6.632 8 2.661 1 5.041 1 6.443 7 2.810 9 4.206 9 6.379 1 1.270 0 5.856 3 6.528 5 2.671 6 4.942 9 6.390 2 2.737 9 4.123 9 6.289 4 1.236 7 表 2 SVM试验参数
训练集样本数 测试集样本数 种群规模 N 最大迭代次数 Tmax/次 交叉验证次数 CV 惩罚因子C取值范围 核函数g取值范围 300 600 10 100 3 [0.01, 100 0] [0.001, 100] 表 3 IGWO-SVM焊缝图像识别结果
算法 CV准确率
δ′(%)准确率
δ(%)收敛代数 运行时间
t′/sPSO-SVM 99.85 98.30 12.1 11.45 GA-SVM 99.96 97.86 50.4 9.80 CS-SVM 100 98.32 11.8 23.24 GWO-SVM 99.98 98.00 4.8 4.75 IGWO-SVM 99.97 99.63 4.1 4.13 表 4 参数均值和标准差对比
算法 惩罚因子C 核函数参数g 平均值 标准差 平均值 标准差 PSO-SVM 222.48 222.16 0.180 4 0.154 0 GA-SVM 103.55 103.06 0.308 3 0.136 8 CS-SVM 558.19 283.66 0.220 4 0.134 2 GWO-SVM 526.00 288.86 0.264 4 0.121 0 IGWO-SVM 358.38 272.84 0.041 7 0.015 9 -
[1] 陈浩, 毛敏, 杨丰全, 等. 免示教六轴焊接机器人在输电线路铁塔塔脚焊接中的应用[J]. 焊接, 2022(1): 55 − 59. [2] 邓钢, 马志, 陈伟光, 等. 多源信息驱动的焊接典型缺陷在线智能识别[J]. 焊接, 2021 (12): 53 − 59. [3] Tian L, Luo Y. A study on the prediction of inherent deformation in fillet-welded joint using support vector machine and genetic optimization algorithm[J]. Journal of Intelligent Manufacturing, 2020, 31(3): 575 − 596. doi: 10.1007/s10845-019-01469-w
[4] Lu X Q, Meng L Z, Chen C, et al. Fuzzy removing redundancy restricted boltzmann machine: improving learning speed and classification accuracy[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(10): 2495 − 2509.
[5] 葛亮, 苗瑞, 葛秋原, 等. 窄搭接焊缝涡流信号的特征提取与缺陷识别[J]. 中国机械工程, 2019, 30(2): 225 − 229. [6] Sun J, Li C, Wu X, et al. An effective method of weld defect detection and classification based on machine vision[J]. IEEE Transactions on Industrial Informatics, 2019, 15(12): 6322 − 6333. doi: 10.1109/TII.2019.2896357
[7] 顾成劼, 杨赟, 杜正春, 等. 基于自适应拟合的小型元件位姿高精度检测算法[J]. 机械设计与研究, 2019, 35(2): 147 − 150. [8] 刘军, 赵剑英, 池云. Zernike矩算法实现焊缝中心线亚像素检测[J]. 沈阳理工大学学报, 2021, 40(4): 1 − 5. [9] Tharwat A, Hassanien A E. Chaotic antlion algorithm for parameter optimization of support vector machine[J]. Applied Intelligence, 2018, 48(3): 670 − 686. doi: 10.1007/s10489-017-0994-0
[10] Xue X. Application of a support vector machine for prediction of piping and internal stability of soils[J]. Geomechanics and Engineering, 2019, 18(5): 493 − 502.
[11] 陈玉喜, 陈华斌, 陈善本. 基于SVM-PSO模型的机器人摆动立焊工艺优化研究[J]. 焊接技术, 2020, 49(5): 66 − 70. [12] 佐磊, 徐相相, 陈昊, 等. 基于改进最小二乘支持向量机的FPGA焊点失效故障评估方法研究[J]. 电子测量与仪器学报, 2021, 35(7): 74 − 82. [13] 杜必强, 孙立江. 基于PSO-SVM模型的焊接转子环焊缝超声缺陷识别[J]. 动力工程学报, 2017, 37(5): 379 − 385. [14] Shi Q, Zhang H. Fault diagnosis of an autonomous vehicle with an improved SVM algorithm subject to unbalanced datasets[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 6248 − 6256. doi: 10.1109/TIE.2020.2994868
[15] 赵丽. 基于改进灰狼算法的焊接车间逆调度方法研究[D]. 武汉: 华中科技大学, 2017. -
期刊类型引用(3)
1. 王梦莹,陆安江,谭叶青,程进. 线结构光焊缝类型识别及特征提取研究进展. 金属加工(热加工). 2024(05): 1-9 .  百度学术
百度学术
2. 李果,张满,朱成彪,万弈,杨大春. 通风管三通相贯线处焊接坡口自动切割机的研究与设计. 科技资讯. 2024(05): 105-107+112 .  百度学术
百度学术
3. 李英顺,于昂,姬宏基,李茂,郭占男. 一种基于KPCA-SCSO -SVM的装甲车发动机状态评估方法. 大连理工大学学报. 2024(04): 426-432 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: