0.   前言

钨极惰性气体保护焊（Tungsten inert gas arc welding，TIG焊）具有焊接过程稳定、焊接质量高等优点，被广泛应用于工业化生产。微TIG点焊是传统TIG焊接的特殊应用，具有焊接电流小、焊接时间短、熔化区域小等特点，广泛应用于微型零件的精密成形制造。焊接电弧作为焊接热源，其物理特性对接头成形过程及性能影响巨大。电弧物理特性的影响因素较多，如钨电极形状^[1]、保护气体^[2]、外加磁场^[3]等，探究不同外界条件对微TIG焊电弧特性的影响规律也显得尤为重要。

为揭示外界条件对电弧物理特性的影响机制，以往研究者常通过采集电弧的电、光、声等信息分析电弧状态^{[4 − 6]}，但电弧等离子体极端的温度条件，使得电弧物理参数难以测得；而使用数值模拟方法可在建立的数学模型下模拟电弧等离子体的流场、温度场和热物理参数等信息^{[7 − 8]}，故也有不少学者采用数值模拟方法研究TIG焊电弧等离子体特性。

微TIG点焊过程焊接电流小、焊接时间短，电弧特性极易受外界因素影响，钨极形状是影响电弧特性的重要因素之一，以往研究者大都通过施加磁场^[1]，叠加高频脉冲电流^[9]等方式改善电弧特性，而在钨极形状对电弧的分析研究较少。近年来有学者从阴极形状出发对TIG电弧特性进行分析研究，如Nahed等人^[10]通过建立二维稳态的磁流体有限元模型，研究了阴极形状中不同尖角、倒角和圆尖角下的电弧等离子体特性，揭示了阴极形状对电弧等离子体的影响机制；雷正等人^[1]通过构建空心钨极TIG焊电弧数值模型，模拟了空心钨极TIG焊电弧的温度场、速度场和压力分布，并对比研究了同条件下空心与实心钨极TIG焊电弧等离子体特性，可见钨极形状显著影响着电弧等离子体特性。钨极形状是微TIG点焊电弧等离子体特性的重要影响因素，然而近年来在钨极锥角对电弧等离子体特性影响机制方面的研究还鲜有报道。

文中假设微TIG焊电弧处于局部热动力学平衡，利用计算流体动力学（CFD）软件ICEM建立了不同钨极尖端锥角微TIG焊二维数学模型；在Fluent软件中采用UDF功能加载惰性保护气的电导率、能量方程源项和动量方程，模拟仿真了稳态直流条件下不同钨极尖端锥角条件下的微TIG电弧的温度场、流场、压力场和电势分布，获得了钨极锥角变化对各电弧物理场的影响规律，分析了电弧等离子体行为变化的原因，并采用试验手段验证了微电弧数值模拟的真实性及模型的适用性。

1.   数学模型

1.1   物理模型及假设

文中建立并计算了不同钨极尖端锥角的TIG焊电弧二维数学模型，依据实际生产经验，选取钨极尖端锥角分别为15°，30°，45°和60°。为简化计算，对电弧模型做如下假设^[11]：①模拟电弧为稳态且二维轴对称；②电弧等离子体是光学薄的，流体状态为层流；③外界环境为标准大气压，惰性气体高纯氩气的密度、黏度、比热容、热导率、电导率和辐射损失仅为温度相关函数；④空间中的等离子体局部为热平衡状态；⑤忽略阳极表面状态对电弧行为的影响；⑥电弧等离子体导电且为不可压缩的牛顿流体。图1为钨极尖端锥角15°的TIG焊数值模型，钨极半径为0.8 mm，电弧长度2.5 mm，钨极尖端为圆台状，钨极凸台半径0.25 mm，采用内孔径9.5 mm、外孔径14 mm的氧化铝材质保护罩，保护罩距阳极板5 mm，钨针露出保护罩2.5 mm，网格使用四边形网格，网格边长尺寸控制在0.025 mm以内，保护气体采用高纯氩气，焊接电流设置为20 A，焊接时间100 ms。

图  1  微TIG点焊电弧数值模型

下载: 全尺寸图片 幻灯片

1.2   控制方程

TIG焊接电弧是一种带电磁流体，满足磁流体力学（MHD）方程组^[12]。在z-r坐标系下，质量守恒方程为

式中：r为径向坐标；z为轴向坐标；u为轴向z速度分量；v径向r速度分量；ρ为惰性保护气体密度。

焊接电弧径向动量守恒方程为^[12]

式中：P为电弧等离子体压力；μ为惰性保护气体黏度。

焊接电弧轴向动量守恒方程为

焊接电弧能量守恒方程为

式中：c_P，k，F_r和F_z分别为惰性保护气体的定压比热容、导热系数、体积力在r方向和体积力z方向的分量，其中F_r=（J×B），F_z=（J×B）_z+ρg，J为电流密度；B为磁感应强度；g为重力加速度。

求解电磁场物理量，需引入电流连续方程^[13]：

欧姆定律：

式中：$\phi $为电势；σ为惰性保护气体电导率；J_r和J_z分别为电流密度的径向与轴向分量。

为计算自感应磁场，引入磁向量势A，其轴向分量A_z与径向分量A_r分别满足：

引入A_Z和A_r，可求得电弧切向感应磁场强度：

1.3   边界条件

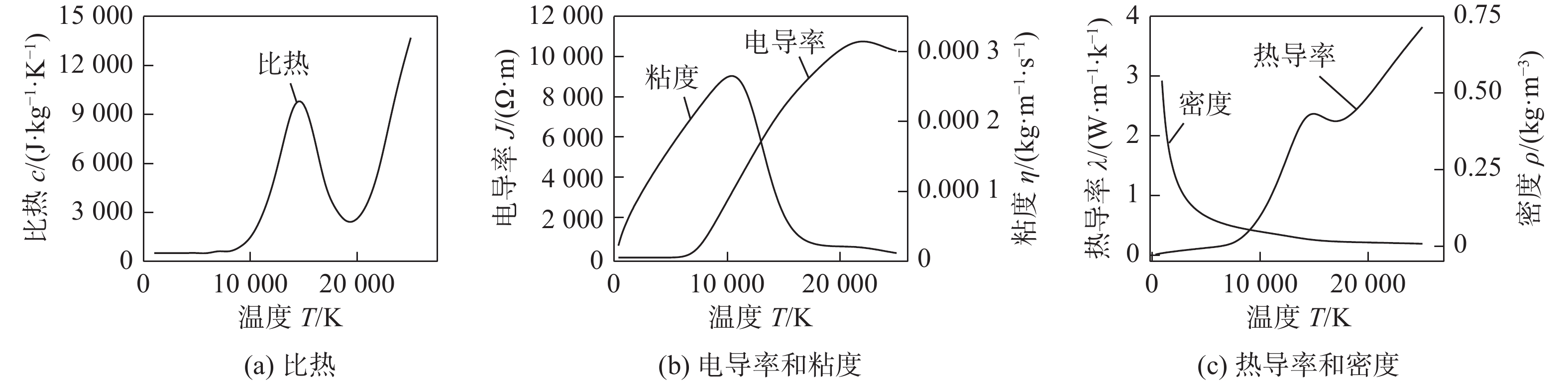
为对微TIG电弧进行数值模拟得出计算唯一解，需对计算域的边界条件和参数进行相关设置，文中采用的电弧模型边界条件见表1。表1中，r为钨极凸台半径，试验时控制氩气流量Q₀=4 L/min,保护罩内孔径为d₁=9.5 mm，钨针半径为r₂=0.8 mm，带入计算公式：氩气气体流量(Q₀) = 流速(v_in) × 截面积(S₁−S₂) ，求得入口流速为0.96 m/s; 由于氩气的电导率在温度小于7 000 K 时很小，为了保证气体处于导电状态，工件表面BC的温度设置为7 000 K，其余壁面温度等边界条件参考石玗等人^{[13 − 15]}的研究设置。微TIG焊采用99.99%纯度氩气作为保护气，在模型电弧区域温度变化范围很大，氩气在不同温度下的物性参数呈高度非线性，其主要物性参数与温度对应曲线如图2所示，通过用户自定义函数（UDF）功能添加氩气25 000 K以下的热物性参数^[16]，该物性参数仅为温度的函数。通过自定义函数DEFINE_SOURCE宏添加源项，使用标量方程添加自定义标量。

表  1  微TIG焊电弧模型边界条件

区域	边界类型	氩气流速v1/(m·s−1)	温度T/K	电势$\phi $/V	磁矢量A/Wb
AB	轴	—	—	—	—
BC	壁面	0	7 000	0	$\partial A/\partial {\textit{z}}= \partial A/\partial r = 0$
CD	压力出口	—	1 000	$\partial \phi /\partial {\textit{z}}= \partial \phi /\partial r = 0$	0
DE	壁面	0	1 000	$\partial \phi /\partial {\textit{z}}= \partial \phi /\partial r = 0$	$\partial A/\partial {\textit{z}}= \partial A/\partial r = 0$
EF	速度入口	0.96	1 000	$\partial \phi /\partial {\textit{z}}= \partial \phi /\partial r = 0$	$\partial A/\partial {\textit{z}}= \partial A/\partial r = 0$
FG	壁面	0	coupled	$\partial \phi /\partial {\textit{z}}= \partial \phi /\partial r = 0$	$\partial A/\partial {\textit{z}}= \partial A/\partial r = 0$
GA	壁面	0	coupled	$ - \sigma \cdot\partial \phi /\partial {\textit{z}}= I/{\text{π}} {r^2}$	$\partial A/\partial {\textit{z}}= \partial A/\partial r = 0$

下载: 导出CSV 

| 显示表格

图  2  氩气物性参数与温度关系

下载: 全尺寸图片 幻灯片

2.   计算结果与讨论

2.1   温度场分布规律

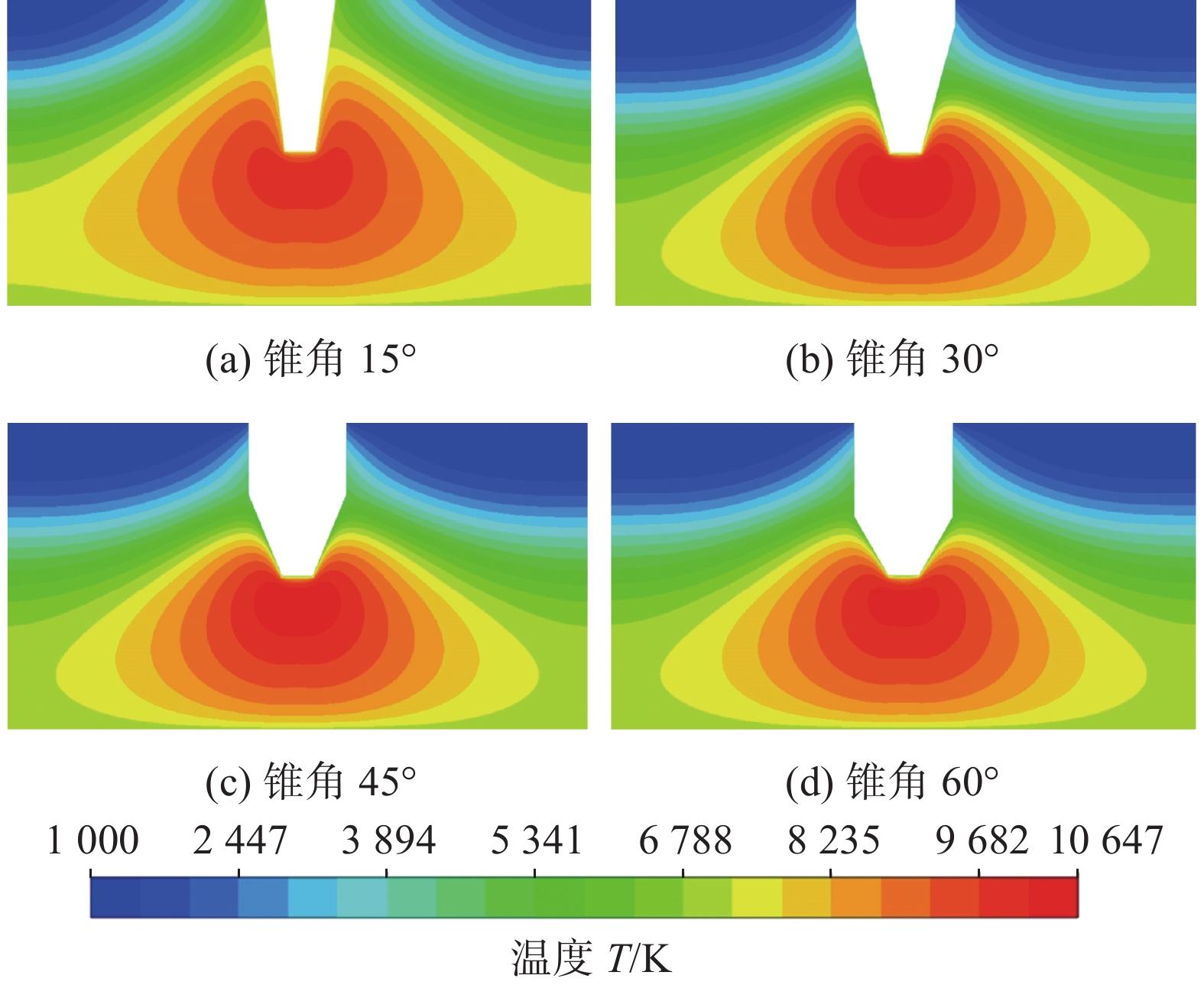
在相同模拟条件下，选取钨极尖端锥角分别为15°，30°，45°和60°进行微TIG点焊电弧温度场、流场、压力场和电势场的模拟，模拟得到的电弧温度场分布云图如图3所示。由图3可知，微TIG点焊电弧呈现钟罩形状。在所有锥角条件下，电弧轴向温度都呈现先增后减规律，越靠近钨极区域温度越高，越靠近板材区域温度越低；电弧径向温度都呈现中间高两边低的类高斯分布。电弧击穿过程的阴极斑点漂移造成电弧在电极尖端蔓延，使得电弧弧柱区扩散，且这种现象随着电极尖端锥角减小越发明显。

图  3  电弧温度分布云图

下载: 全尺寸图片 幻灯片

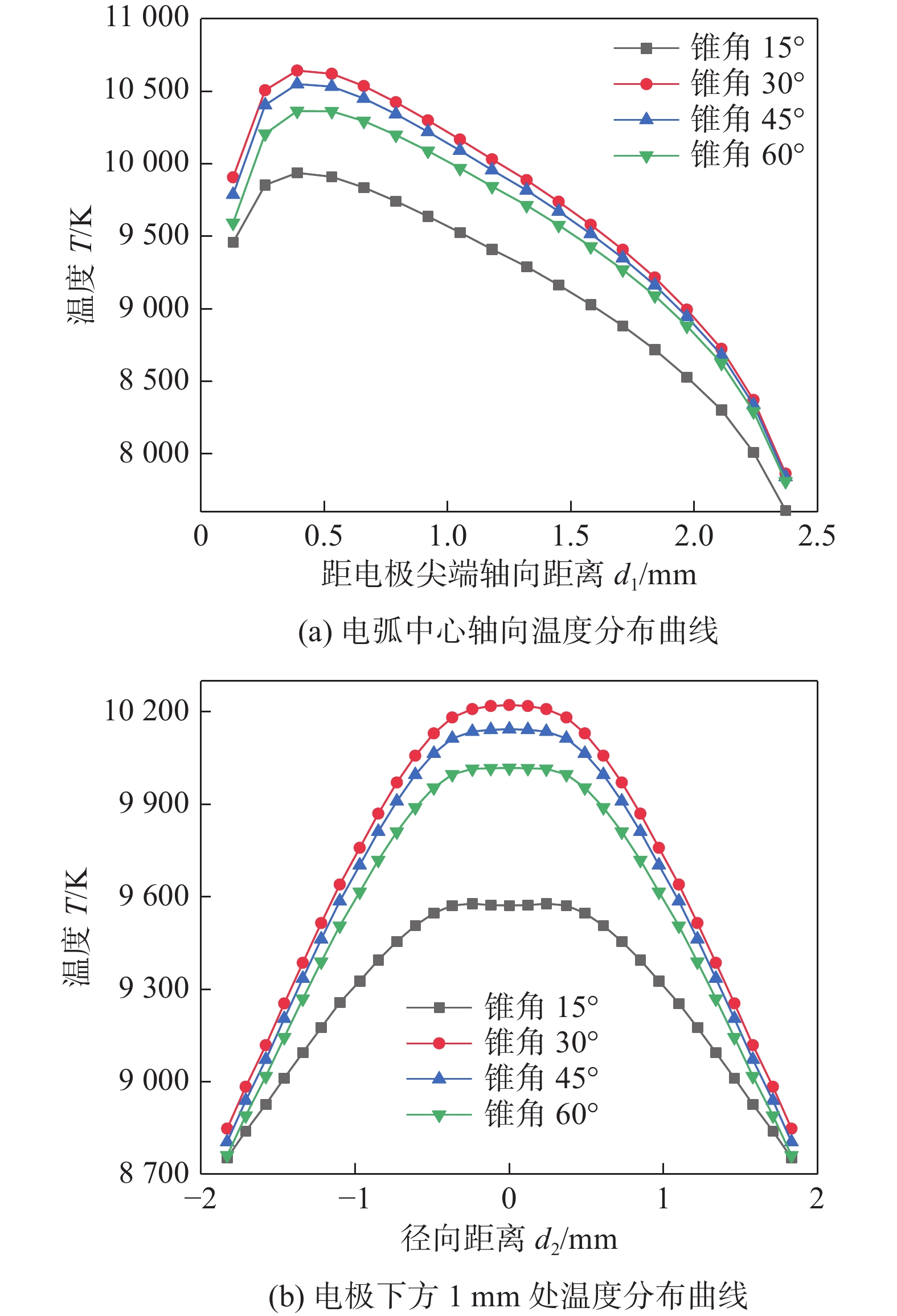
不同锥角条件下，电弧轴向和径向温度分布曲线如图4所示。由图4(a)可知，不同锥角条件下电弧中心轴向温度分布曲线皆呈现先增加后减小的变化趋势，各钨极锥角电弧温度均在钨极尖端下方约0.45 mm处达到最高，随后保持下降，下降速度先慢后快。钨极尖端锥角为15°，30°，45°和60°时的电弧温度峰值分别为9 940 K，10 647 K，10 555 K和10 375 K，温度峰值最高较最低高出约707 K。当锥角由60°减至30°时，钨极尖端导电截面半径减小，导致电流密度增大，单位面积产生的焦耳热量增多，使电弧温度峰值增高；当锥角由30°减至15°时，电弧温度峰值明显下降的原因是，一方面，锥角的减小伴随电弧上爬现象的出现，使钨极尖端导电面积增大，电流相同时，平均电流密度减小，且电弧收缩力减小，电弧弧柱扩散使电弧温度降低；另一方面，从后文电势场结果可知，锥角减小造成电弧电势差减少，阴阳极间的电流密度降低，电弧单位面积产生的焦耳热量减小，使得电弧温度峰值降低。

图  4  电弧温度分布曲线

下载: 全尺寸图片 幻灯片

由图4(b)电极下方1 mm处温度分布曲线可知，不同钨极锥角条件下的电弧径向温度分布曲线皆呈现中间高两边低的类高斯分布规律，电弧温度在中间轴线处维持较高温度，后随着径向距离的增加电弧温度迅速下降。随着锥角减小，钨极导电截面半径导致电流密度增大，电磁收缩力对电弧约束增大，导致图4(b)中锥角由60°减至30°时电弧温度下降曲线变陡；随着钨极锥角继续减小，电弧上爬现象严重，钨极导电面积增大，平均电流密度减小，单位面积产生的热量减小，且电磁收缩力对电弧约束减小，使锥角由30°减至15°时电弧温度下降变缓。可见钨极锥角的变化导致钨极尖端导电面积改变，显著改变电弧电流密度及电磁收缩力，进而影响微TIG电弧温度场。

2.2   流场分布规律

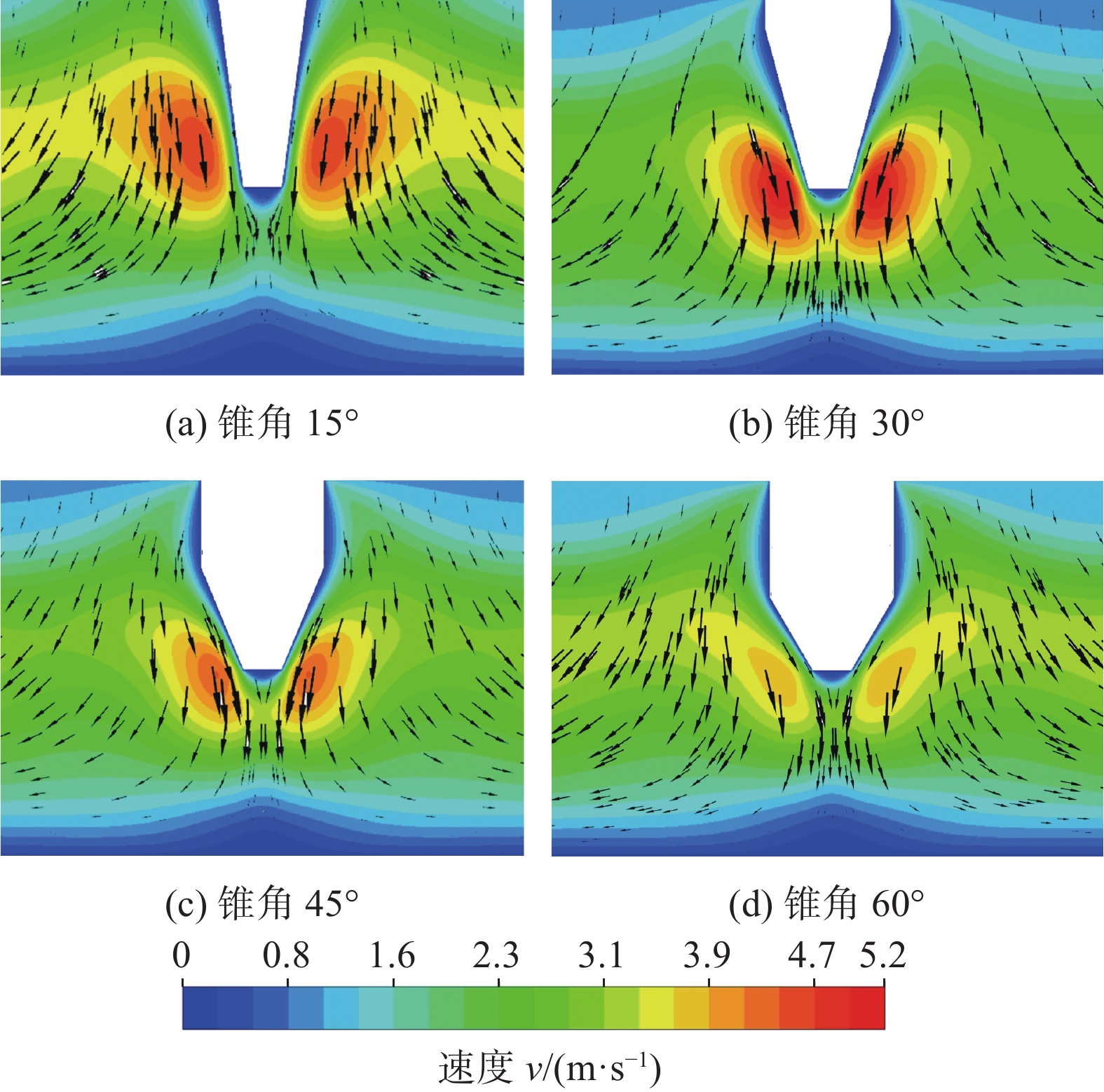
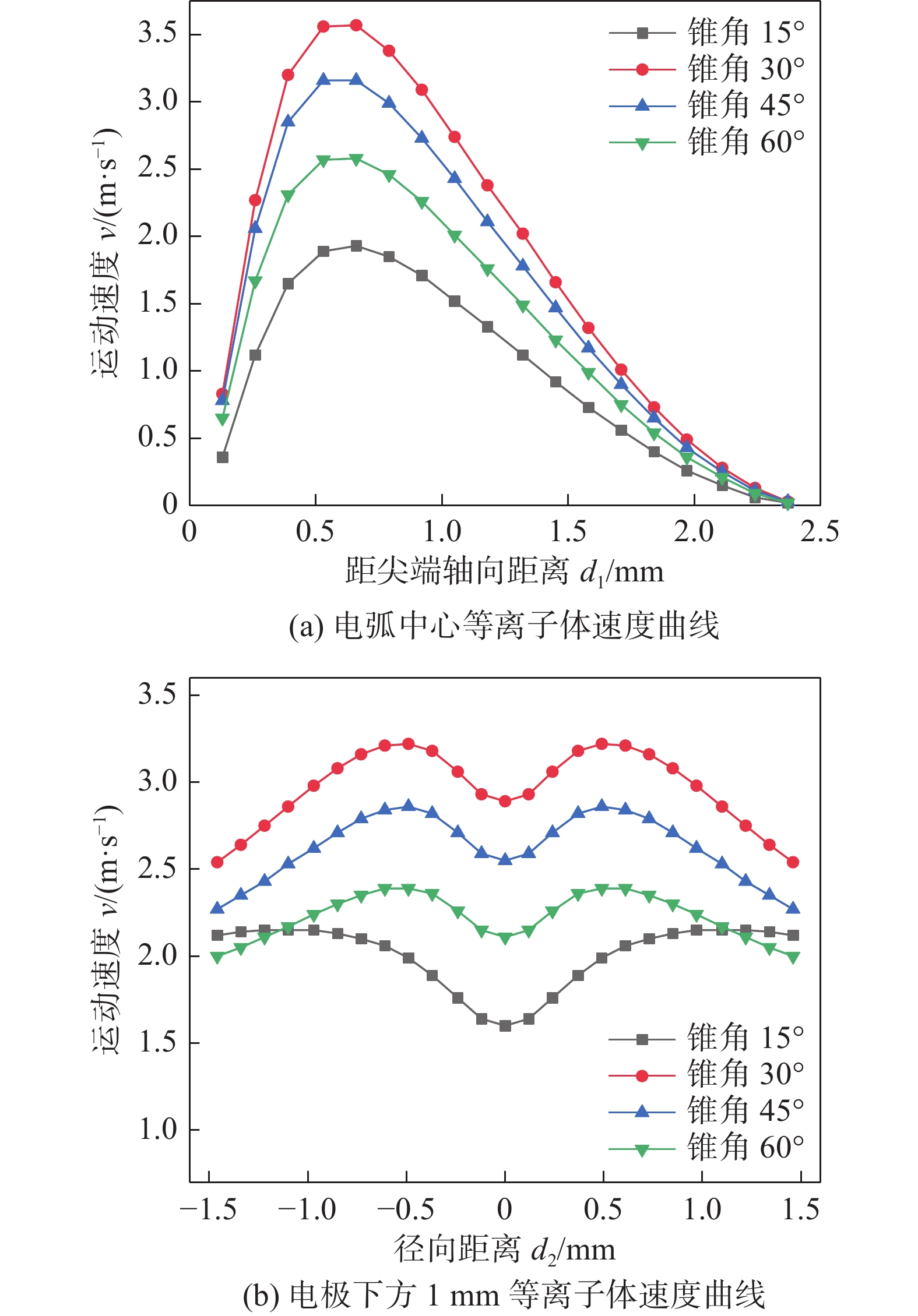
图5为模拟得到的不同钨极锥角条件下微TIG点焊电弧等离子体运动速度分布云图。由图5可知，不同锥角条件下电弧等离子体运动速度高速区域均集中在钨极尖端外侧周围，造成此现象的原因是小电流条件下钨极尖端电流密度较小，电磁收缩力作用下的电弧等离子体动量增加缓慢^[15]，使试验中微TIG电弧呈扩散趋势。当锥角由60°减至30°时，钨极尖端导电截面半径缩小，电流密度增大，电磁收缩力作用下的等离子体动量大幅增加，导致图5(b)中等离子体分布更加集中且运动速度峰值更高；当锥角继续减小至15°，受钨极阴阳极间尖端导电截面积增大影响，平均电流密度减小，电磁收缩力作用下的等离子体动量增加变缓，导致图5(a)中等离子体分布扩散且运动速度峰值降低。

图  5  电弧等离子体运动速度分布云图

下载: 全尺寸图片 幻灯片

不同锥角条件下，电弧等离子体运动速度分布曲线如图6所示。由图6(a)电弧中心等离子体速度曲线可知，在电极尖端下方，不同锥角条件下电弧中心轴向等离子体在电磁力的作用下速度均快速增加，在距钨极尖端约0.6 mm处达到最高，随后缓慢下降并在阳极处减至0 m/s。钨极尖端锥角为15°，30°，45°和60°时的电弧等离子体中心轴线上的速度峰值分别达到1.9 m/s，3.5 m/s，3.1 m/s和2.5 m/s，等离子体速度峰值最高较最低高出1.8 m/s，约高出一倍。当锥角由60°减至30°时，钨极尖端导电截面半径缩小，平均电流密度增大，等离子体流力和电磁收缩力作用下，等离子体动量大幅增加使锥角30°时的等离子体速度增幅最高且保持在较高水平；随着锥角继续减小至15°，电弧上爬现象的出现引起钨极尖端导电面积增大，使平均电流密度减小，等离子体流力和电磁收缩力作用下等离子体动量增幅减缓且保持在较低水平。

图  6  电弧等离子体运动速度分布曲线

下载: 全尺寸图片 幻灯片

由图6(b)电极下方1 mm等离子体速度曲线可知，在径向等离子体运动速度分布上，不同锥角条件下的电弧等离子体运动速度均随径向距离增加先有所增加，后保持缓慢下降趋势。此现象是因为微TIG点焊焊接电流小，电磁收缩力较小，等离子体流力的径向分力作用下使等离子体速度出现先增后减现象。从图6(b)可知，锥角为30°的电弧等离子体速度下降最快，即电弧最收缩，验证了钨极锥角减至30°时，电弧电流密度达到最高值，电磁收缩力的轴向分力增大导致等离子体在径向方向上的速度下降增快。可见钨极锥角的变化显著影响着等离子流力和电磁收缩力对等离子体动量的作用，进而影响电弧流场分布。

2.3   压力场分布规律

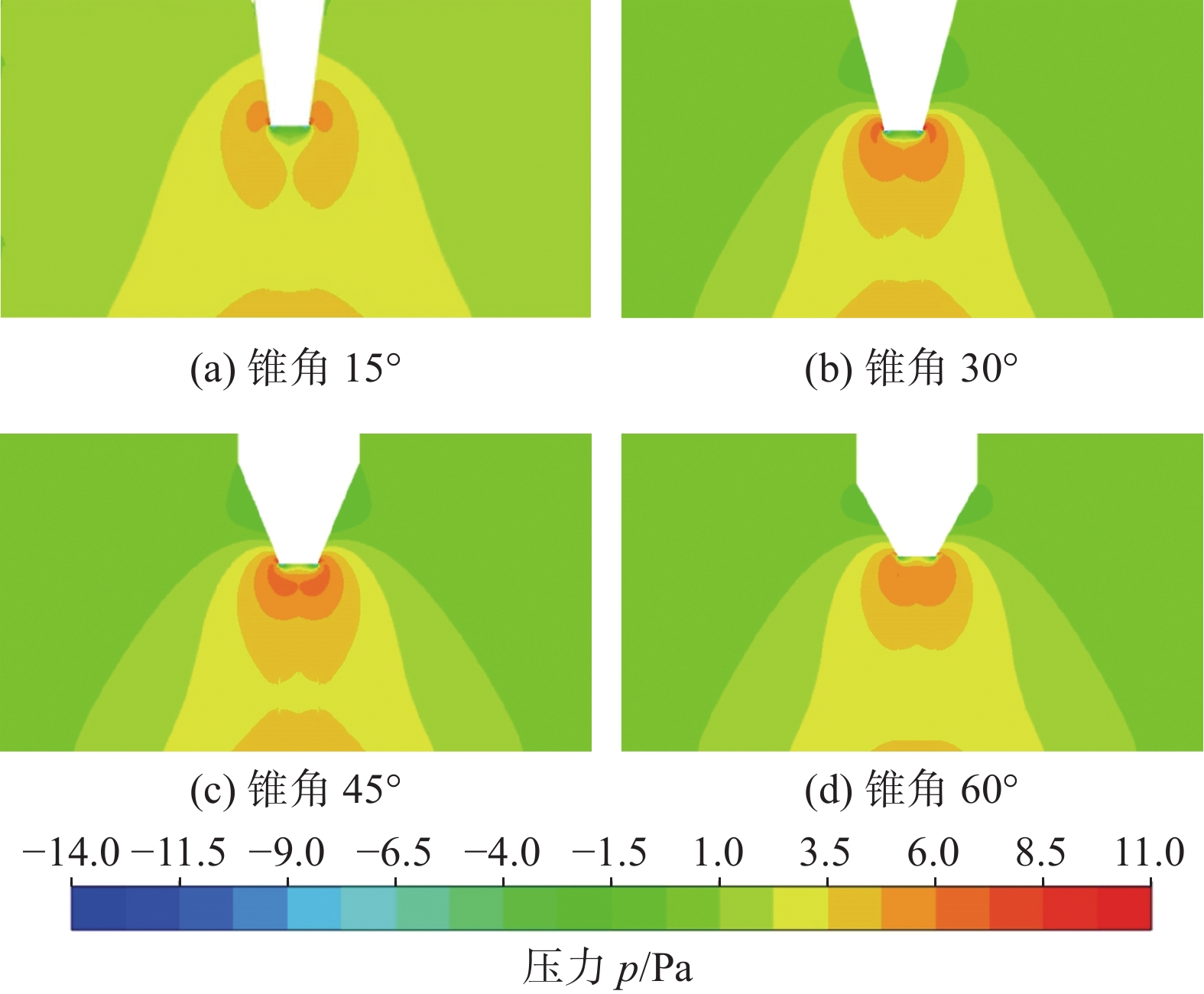
图7为不同钨极锥角条件下微TIG点焊电弧压力分布云图。从图7可知，从阴极到阳极，不同锥角条件下的电弧高压区均集中在电极尖端，随着向阳极移动出现平稳的过渡区域，最后在阳极上方附近电弧压力有小幅回升，压力分布与雷正等人^[1]研究中的实心钨极压力分布相似。当锥角为15°和30°时，钨极尖端母线与轴线的夹角较小，母线与台面夹角处的电流密度增高，电磁收缩力增加使电弧压力出现峰值；随着锥角增大，钨极尖端母线与轴线的夹角增大，母线与台面夹角处的电流密度减小，压力峰值减小并向钨极下方移动。

图  7  电弧压力分布云图

下载: 全尺寸图片 幻灯片

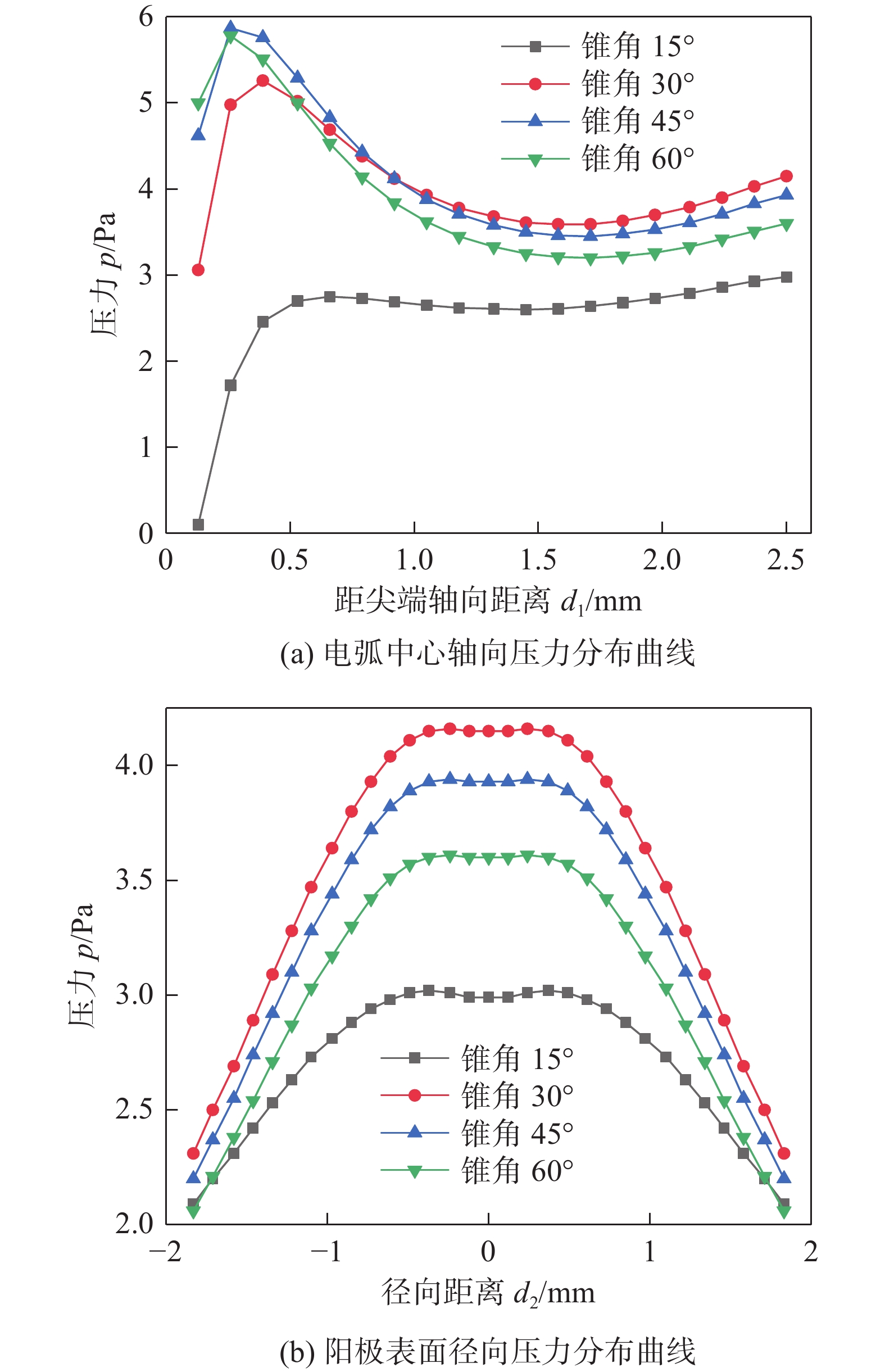
不同锥角条件下，电弧轴向和径向压力分布曲线如图8所示。由图8(a)电弧中心轴向压力分布曲线可知，不同锥角条件下电弧压力皆在钨极尖端下方约0.35 mm处达到最大值，随后电弧压力缓慢下降，在到达距离阳极表面约1 mm处，电弧压力有小幅回升。结合图7可知，钨极锥角为15°，30°，45°和60°时的电弧压力峰值分别为7.3 Pa，11.3 Pa，9.1 Pa和7.0 Pa，压力峰值最高较最低高出约54.7%。锥角由60°减至30°时，锥角的减小使钨极尖端导电半径缩小，导致电流密度增大，电磁收缩力增大提高了等离子体动量增量进而使电弧等离子体压力增高。当锥角继续减至15°时，钨极尖端电弧上爬现象严重，使钨极导电面积增大，平均电流密度减小，电磁收缩力作用下的等离子体动量增加减缓使电弧压力峰值减至7.3 Pa。

图  8  电弧压力分布曲线

下载: 全尺寸图片 幻灯片

由图8(b)阳极表面径向压力分布曲线可知，不同钨极锥角条件下的电弧阳极表面径向压力分布曲线皆呈现中间高两边低的类高斯分布规律，阳极压力均在轴线附近保持最高水平不变，随后开始大幅下降。钨极锥角为15°，30°，45°和60°时的电弧阳极压力峰值分别为2.98 Pa，4.15 Pa，3.93 Pa和3.60 Pa，阳极表面压力峰值最高较最低高出39.2%。当钨极锥角由60°减至30°时，一方面，钨极尖端导电截面半径减少，电流密度和电磁收缩力增大，等离子体动量增幅更高且更加收缩，导致图8(b)中阳极表面压力分布更加集中且压力峰值更高；另一方面，钨极尖端锥角变小可以减小补充气流的阻力，有利于提高阳极表面压力。当锥角继续减至15°时，钨极尖端电弧上爬使钨极导电面积增大，平均电流密度和电磁收缩力减小，等离子体动量增幅减缓，导致图8(b)中阳极表面压力更为分散及压力减小。可见钨极锥角变化显著改变了电磁收缩力和补充气流的阻力，进而影响阳极表面压力分布。

2.4   电势场分布规律

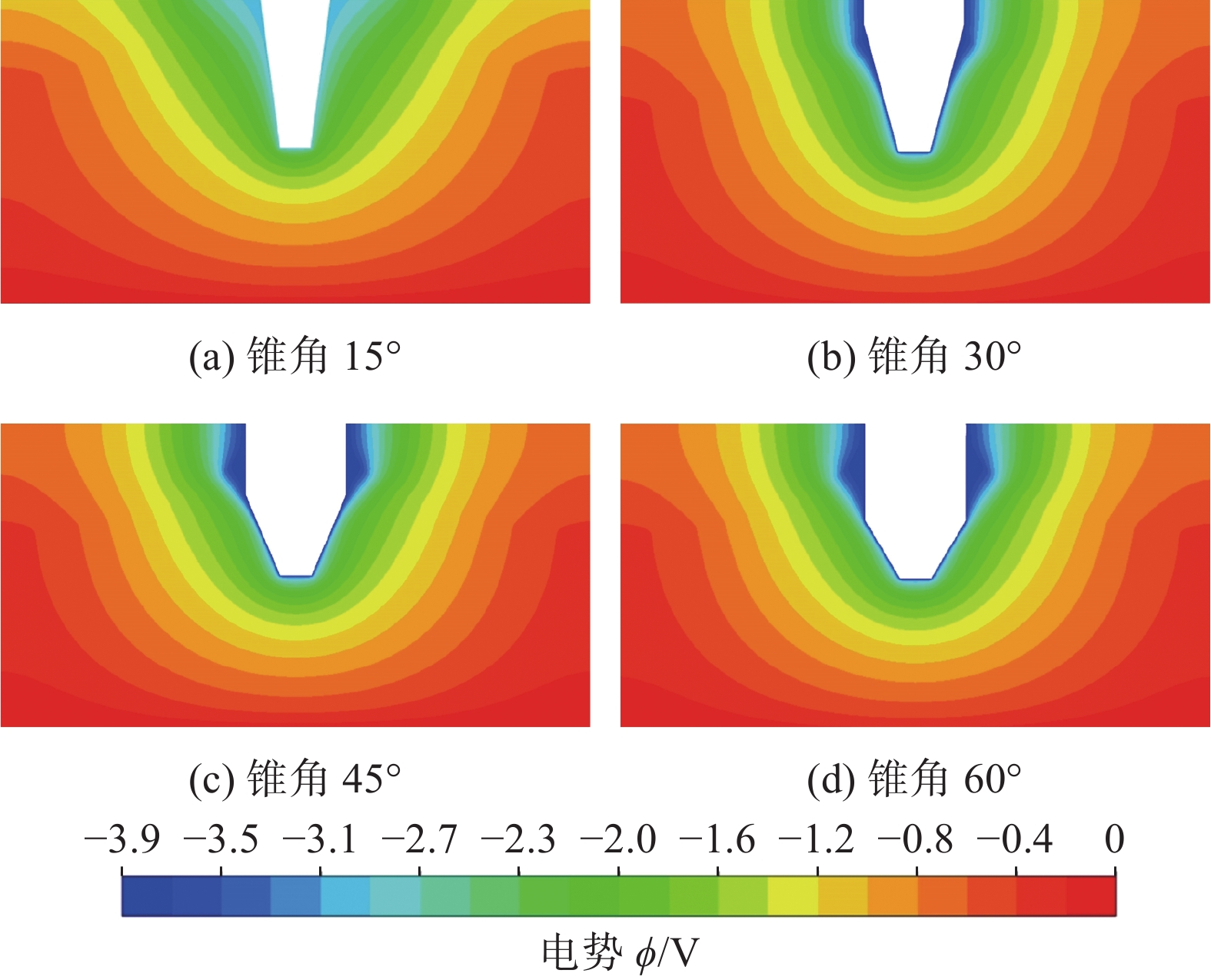
图9为不同钨极锥角条件下微TIG点焊电弧空间电势分布云图。设定工件阳极电势为0，电势从阴极到阳极逐渐升高，因此电弧空间电势为负值。由图9可知，电势在中心轴线区域的变化梯度最大，即电流密度最大，电势分布趋势与刘政军等人^[2]研究中的电势分布类似；钨极锥角由60°减至30°时，钨极尖端导电截面半径缩小使等势线更密集，即电流密度更高；当锥角减至15°时，电弧上爬引起钨极导电面积增大使等势线分布扩张，平均电流密度减小。

图  9  电弧电势分布云图

下载: 全尺寸图片 幻灯片

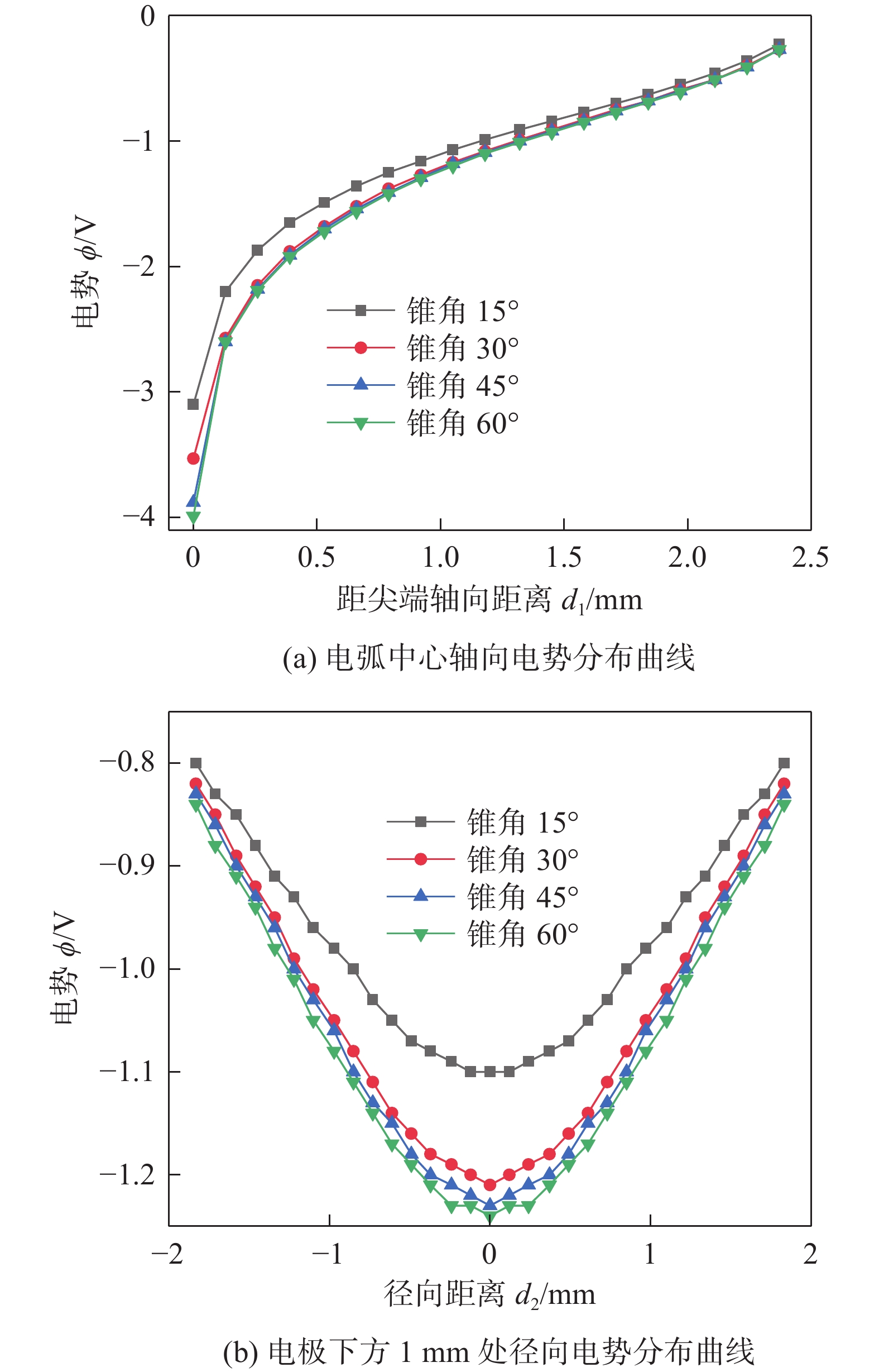
不同钨极锥角条件下，电弧轴向和径向电势分布曲线如图10所示。由图10(a)电弧中心轴向电势分布曲线可以看出，锥角为15°，30°，45°和60°的电弧钨极表面电势分别为−3.1 V，−3.8 V，−3.9 V和−3.9 V，阴极与阳极间电势差最高较最低高出约25.8%，阴阳极间电势差随锥角减小先处于平稳状态，随后有所下降。阴阳极电势差减小，等离子体所受电磁收缩力减小，使电弧等离子体动量增幅变缓，等离子体运动速度和阳极压力降低。从图10(b)看出，在同一径向平面上，不同锥角条件下的电弧电势均在距中心轴线0～±0.25 mm范围内稳定保持在较低水平，随后呈快速上升趋势。可见钨极锥角的改变导致电势分布产生变化，电势分布的改变直接影响着电弧等离子体动量及电弧温度场分布。

图  10  电弧电势分布曲线

下载: 全尺寸图片 幻灯片

3.   验证试验

3.1   电弧形态试验验证

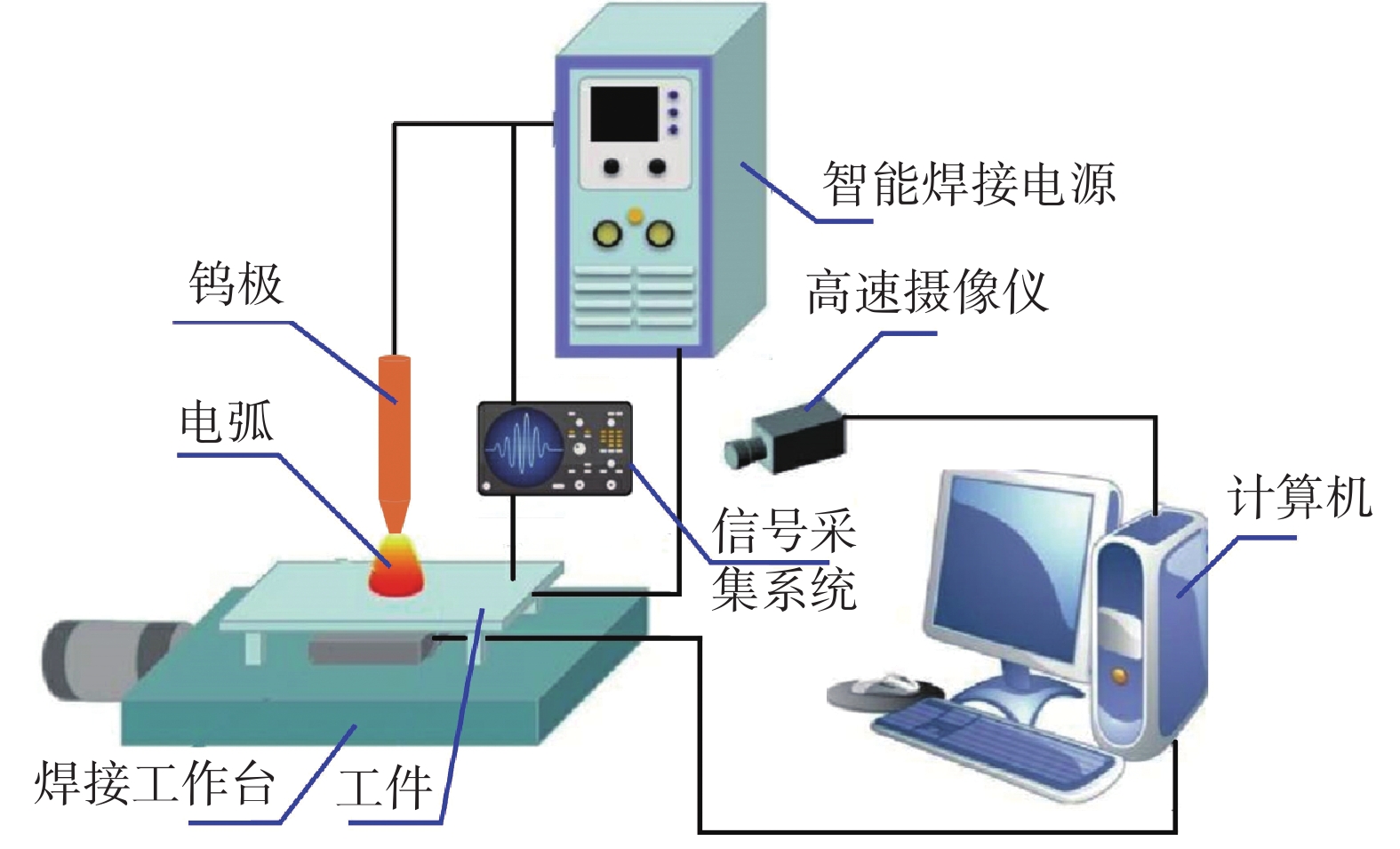
实际焊接过程中，电弧内部的流场和温度场是复杂变化的，很难实现对其内部温度及等离子体流速的测定。文中通过高速摄影仪采集的焊接过程中微TIG电弧形态验证建立模型的准确性^[1,8,12,16]。图11为搭建的基于微TIG点焊的电弧形态采集系统。

图  11  微TIG点焊电弧形态采集系统

下载: 全尺寸图片 幻灯片

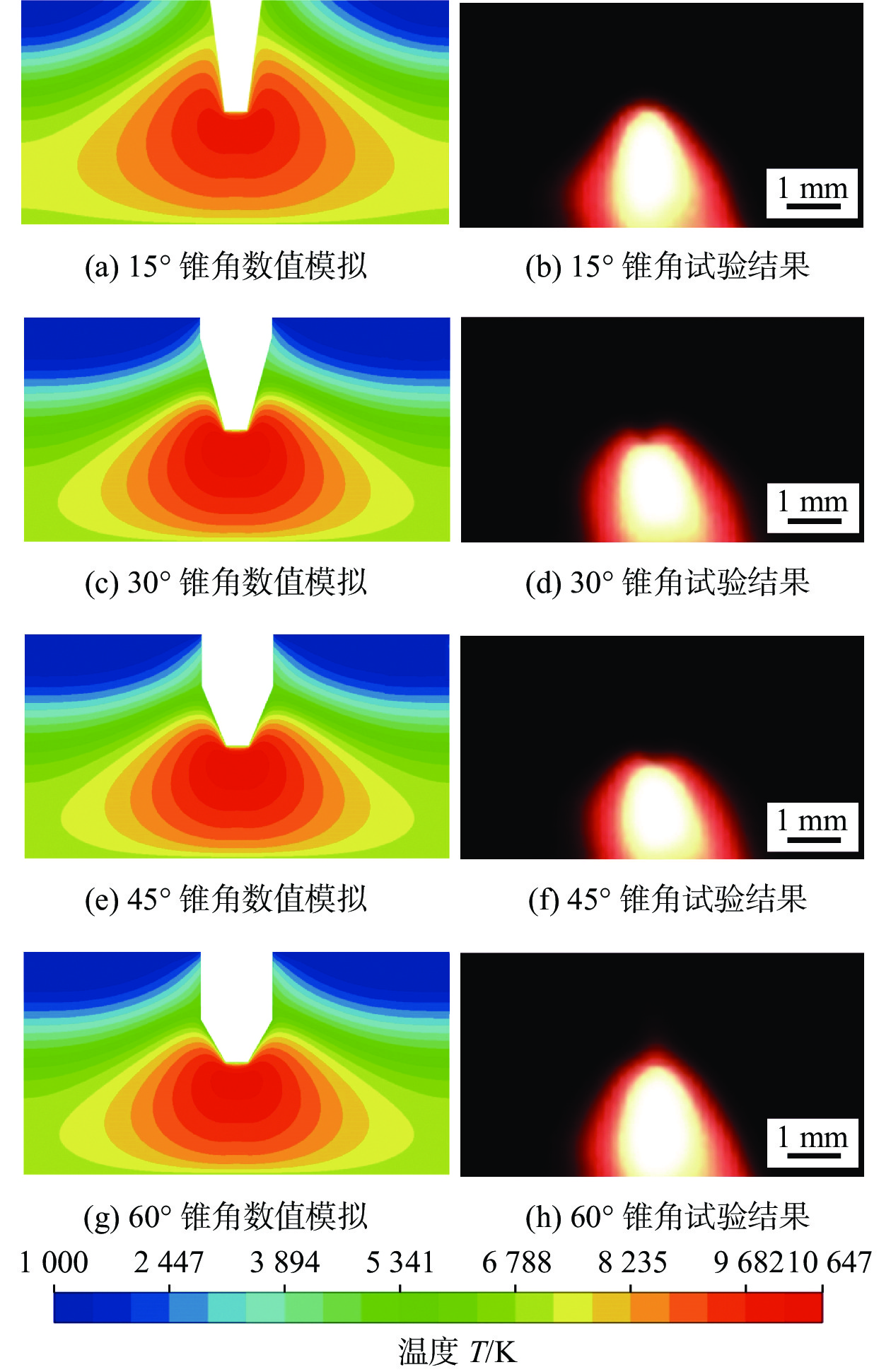
试验采用与电弧模拟相同的焊接参数，保护气使用99.99%纯度氩气，试验工艺参数见表2。焊接电源选用自制智能TIG点焊电源，拍摄选用IDT Y4-S2系列高速摄影仪，采样频率为4 500 Hz，曝光时间220 μs；滤光片中心波长所测的特征谱线应满足分辨率高、半高宽窄、强度高，光谱常数不确定度小等条件，结合文献[9]中张刚等人研究中滤光片的选取规则和文献[17]中赵洪志等人研究中的TIG焊电弧等离子体光谱信息，选取NBP650 nm窄带滤光片。图12为锥角为15°，30°，45°和60°时数值模拟和实际拍摄的微TIG电弧对比图。可见当锥角由60°减至30°时，由于导电截面半径的减小使平均电流密度增加，电弧弧柱明显收缩，且电磁收缩力对钨极尖端处的电弧压缩作用更为明显；锥角由30°减至15°时，试验电弧有明显的上爬现象，且电弧弧柱有扩散趋势，与数值模拟结果相符。考虑到实际焊接中，电弧受焊接环境等因素的影响，在进行数值模拟时进行了一定简化，相比实际情况，数值模拟会产生一定误差，通过对比分析，微TIG电弧模拟结果与试验电弧形态相吻合，可用来描述焊接过程中电弧多物理场。

表  2  焊接试验参数

焊接电流 I/A	气体流量 Q0/(L·min−1)	缓升时间 t1/ms	持续时间 t2/ms	弧长 l/mm
20	4	0	100	2.5

下载: 导出CSV 

| 显示表格

图  12  微TIG点焊电弧形态的数值模拟和试验结果对比

下载: 全尺寸图片 幻灯片

3.2   电弧电压试验验证

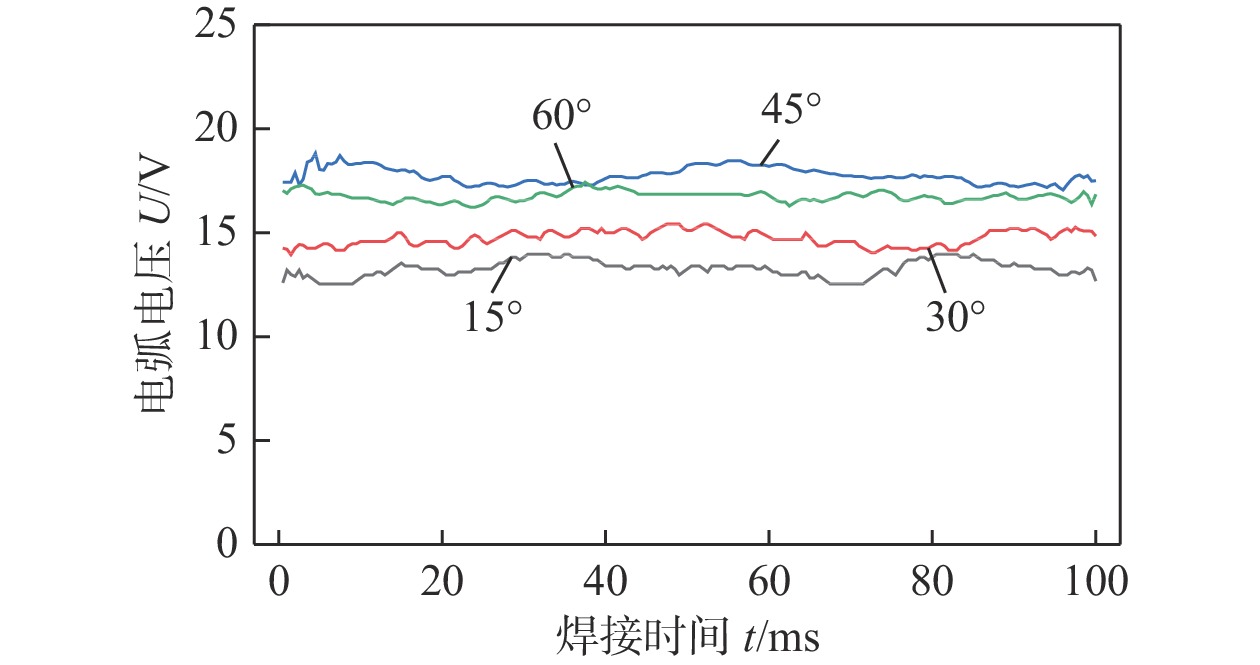
在微TIG点焊试验中，因焊接电源通过高频高压方式引弧，直接使用示波器对电弧电压测量会造成示波器损坏，因此通过安装霍尔电压传感器方式对电弧电压进行采集。焊接试验工艺参数见表2。考虑到微TIG焊接环境的复杂性，电弧对试验采集信号存在干扰，在采集电压时，采集点选取焊接电源正负极两端，所以采集电压由电弧电压、钨针端电压、引弧器端电压和工件间电压共同构成，经过滤波后不同锥角下的电压数据如图13所示。由图13可知，各锥角下的测量电压在焊接过程中均整体保持平稳趋势，锥角由60°减至45°时，电压变化不大，当锥角继续由45°减至30°和15°时，所测电压有明显下降趋势；不同锥角下，所测电压平均值最高较最低约高出30%，与数值模拟电势场中阴阳极间电势差变化趋势一致，这也从侧面验证了模拟结果的准确性。

图  13  不同锥角下微TIG点焊电弧电压

下载: 全尺寸图片 幻灯片

4.   结论

（1）钨极锥角减小使导电截面半径减小，导致电流密度增加，电磁收缩力增加，使电弧单位面积产生的焦耳热增多，电弧温度增高；另外，钨极锥角越小，电弧上爬现象严重，使钨极导电面积增大，平均电流密度有减小趋势，电弧有扩张趋势，电弧温度有所下降。

（2）微TIG电弧中，电弧电流密度较小，电磁收缩力较小，等离子体流力的径向分力对电弧产生的扩张作用明显，使电弧呈现扩张趋势。等离子体流力和电磁收缩力作用下，等离子体运动速度和阳极表面压力均随锥角减小呈先增大后减小的趋势。

（3）微TIG点焊电弧形态试验中，锥角15°的微TIG电弧上爬现象明显，电弧能量降低且出现扩张趋势；锥角30°的微TIG电弧弧柱在电磁收缩力的作用下最为收缩；电弧电压采集试验中，不同锥角下所测电压与数值模拟电势场中阴阳极间电势差变化趋势一致，也从侧面验证了数值模拟的准确性。