Effect of additional wire on temperature field of swing-arc narrow gap GMA welding
-
摘要:目的
旨在建立主辅丝同步的摇动电弧窄间隙GMA焊温度场模型。
方法从宏观传热学出发，综合考虑横断面几何形状特征、主丝和辅丝的运动及焊缝表面形状对电弧热流分布特征的影响，并利用ANSYS软件对不加辅丝和主辅丝同步摇动两种情况下的电弧瞬态温度场及热循环曲线进行了模拟计算。
结果焊缝横断面的计算结果、测温特征点热循环曲线的计算结果，与试验结果接近。
结论证明模型可以真实反映添加辅丝的摇动电弧的移动轨迹及分布特征，具有较高的准确性。不加辅丝时，焊缝横断面底部有明显“双峰”特征，主辅丝同步摇动时，“双峰”特征明显减弱。主辅丝同步摇动情况下的热影响区宽度略有增加。
Abstract:[Objective] The purpose is to develop the heat source model for swing-arc narrow gap GMA welding. [Methods] This paper considers the influence of arc swing, geometric feature of welded joint, movement of additional wire and weld surface shape on arc heat flux distribution, based on macro thermal transfer theory and geometric feature of weld cross section. By using ANSYS software, the transient temperature profile and thermal cycle curve in swing-arc narrow gap GMA welding are calculated and their distribution features are analyzed. [Results] The results show that the established heat source model can reflect the moving path of swing-arc and its thermal action feature, the calculated geometry and size of weld cross section and thermal cycles of temperature measurement characteristic point agree well with the experimental data. [Conclusion] It is proved that the model can truly reflect moving track and distribution characteristics of swing-arc with additional wires, and has high accuracy. There is an obvious “double peak” feature at the bottom of the cross section of the weld without additional wire, while the “double peak” feature is diminished with additional wire. The width of HAZ slightly increases when the main and additional wires are synchronously swing.
-
0. 前言
新型摇动电弧窄间隙GMA（Gas metal arc）焊，通过空心轴步进电机驱动微弯型导电杆绕焊炬中心线往返旋转，使焊丝在工件坡口内作圆弧形的来回摇动，以实现窄间隙焊接[1]。为了进一步提高焊接效率，Wang等人[2 − 5]在主丝摇动的基础上，添加了同步摇动的辅丝，使其具有效率高、接头性能优异等特点，是厚板较为理想的焊接方法。温度场对接头性能具有重要影响，相对于薄板的焊接，厚板的温度场更为复杂，而添加了辅丝之后，辅丝的熔化和过渡也会对工件的温度场产生影响，使温度场分析更为复杂，通过对其温度场的研究，可以深入了解焊接内部物理现象，对工艺参数的优化，具有重要意义。
目前，对摇动电弧窄间隙GMA焊设备、工艺研究的论文较多，而对于内部物理机制研究的论文较少，添加辅丝的则更为甚少。Wang等人[6 − 8]通过试验的方法分析了不同工艺参数对焊缝成形的影响。随着数值分析的不断完善，数值模拟已成为物理过程研究的重要手段之一[9 − 10]，Serizawa 等人[11]采用有限元对厚壁管窄间隙TIG焊进行了数值模拟和计算，分析了热输入对坡口间隙收缩的影响。胥国祥等人[12]建立了摇动电弧窄间隙GMA焊温度场模型，并利用ANSYS软件计算了焊温度场，但此模型没有添加辅丝。文中在该模型的基础上，综合考虑横断面几何形状特征、主丝和辅丝的运动及焊缝表面形状，建立了添加辅丝的摇动电弧窄间隙GMA焊温度场模型，并利用ANSYS软件计算了焊接温度场，分析了辅丝对温度场分布的影响，为了解其物理机制、工艺改进等提供理论支撑。
1. 试验材料和方法
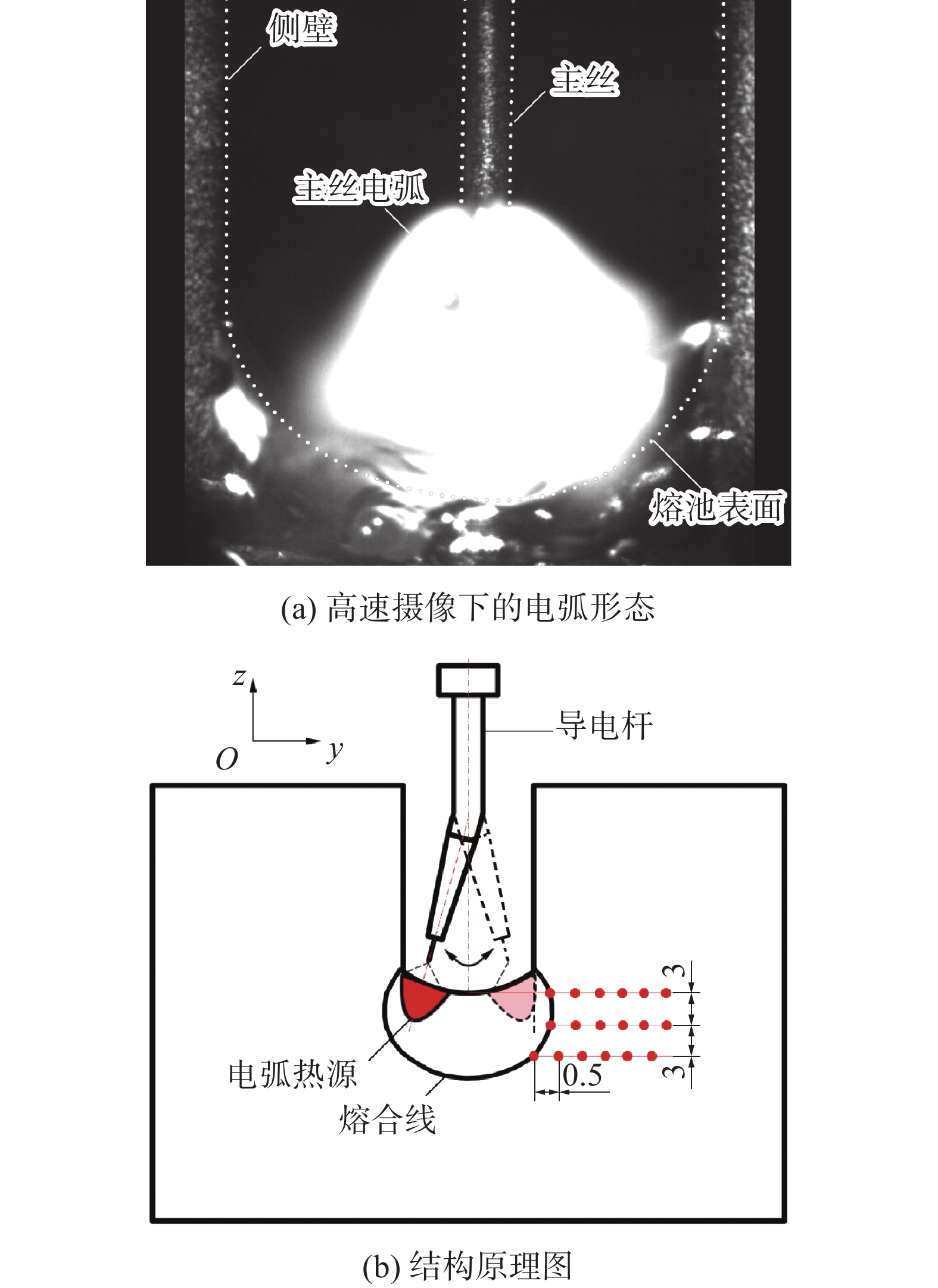
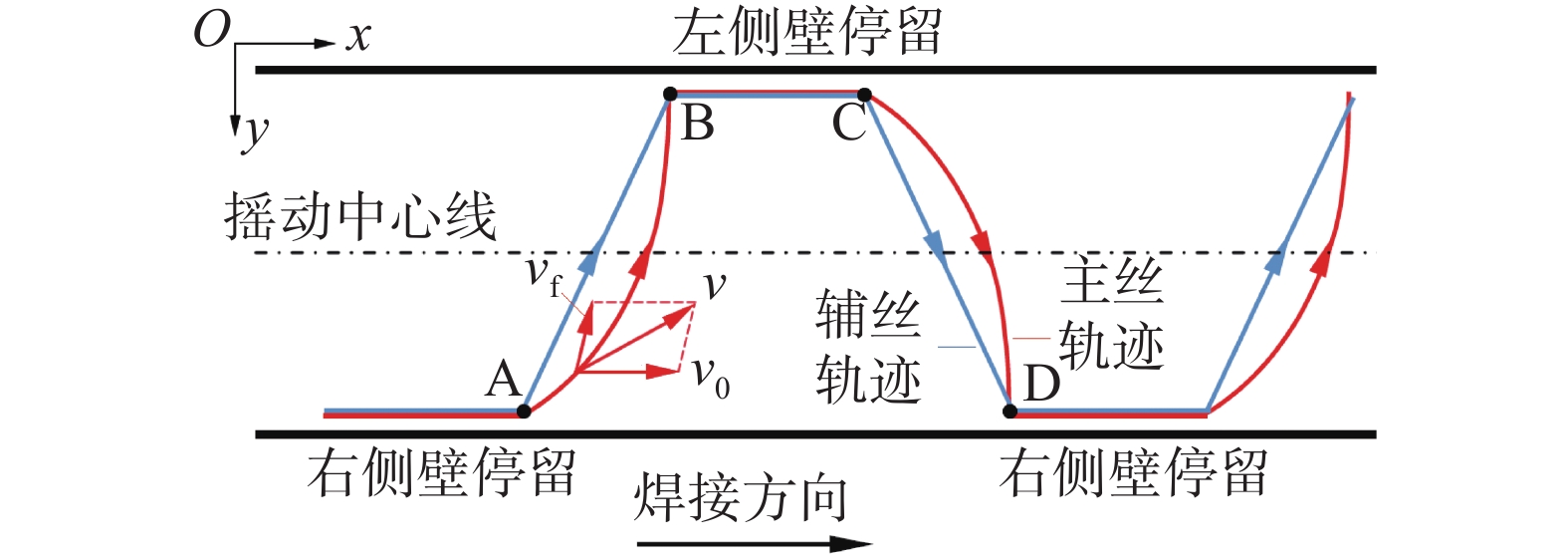
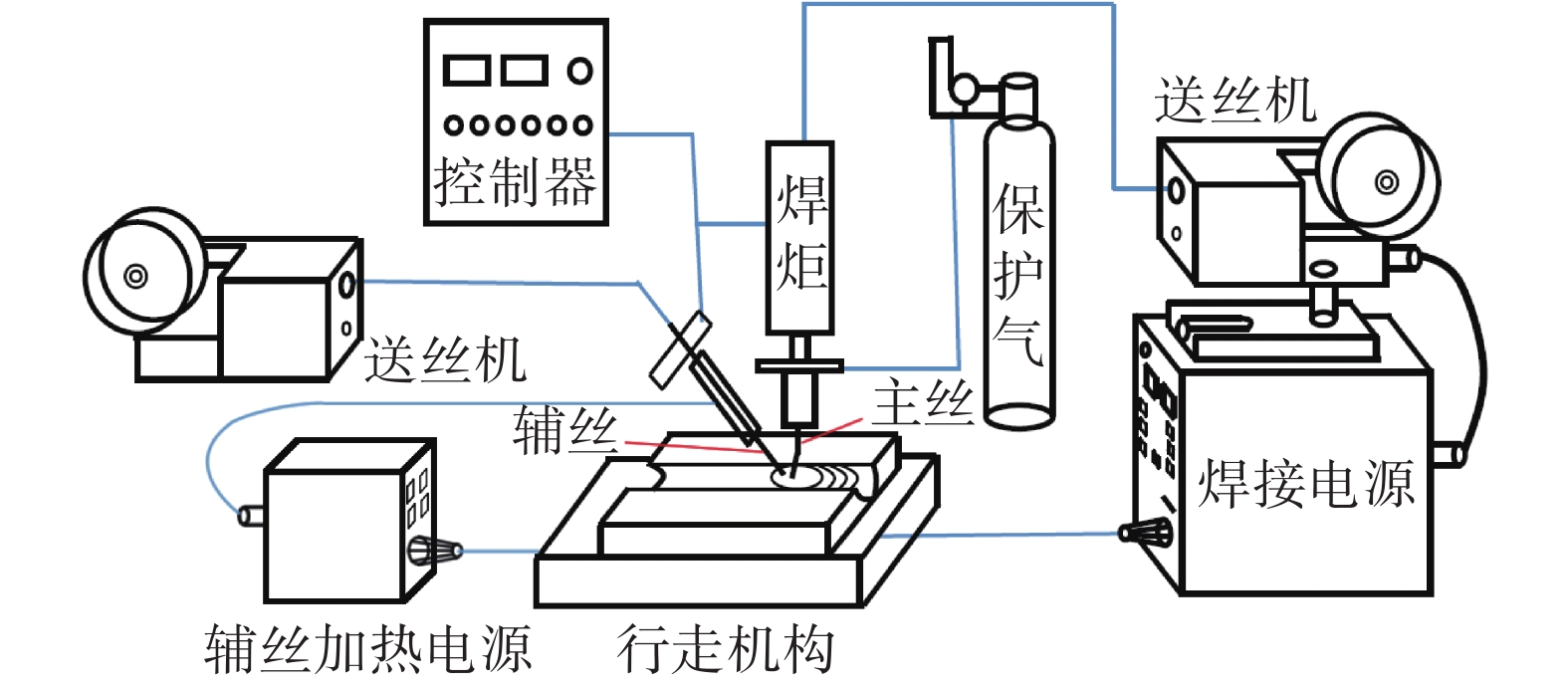
图1为摇动电弧窄间隙GMA焊系统原理示意图，主丝和试件之间产生电弧，而辅丝和试件之间并不产生电弧，辅丝在前，主丝在后，即为双丝单电弧焊接，焊接系统实物图如图2所示。图3(b)为摇动电弧窄间隙GMA焊结构原理图，焊接时，微弯导电杆绕其中心旋转轴旋转，从而驱动主丝端部在一定角度范围内摇动。同时焊炬始终以给定的速度$ {v}_{0} $沿着焊接方向x移动，图4为主丝和辅丝移动轨迹。主丝由右侧A点摇动到左侧B点后，主丝停止摇动并以$ {v}_{0} $沿着焊接方向x移动一段时间至C点，而后又继续摇动至右侧D点。通过控制器使辅丝跟随主丝摆动，且辅丝与主丝在y方向上的坐标始终保持一致，同时辅丝以$ {v}_{0} $的速度沿着焊接方向x移动。
![]()
图 1 添加辅丝的摇动电弧窄间隙GMA焊系统原理示意图Figure 1. Diagram of the SA–NG–GMAW system with additional wire![]()
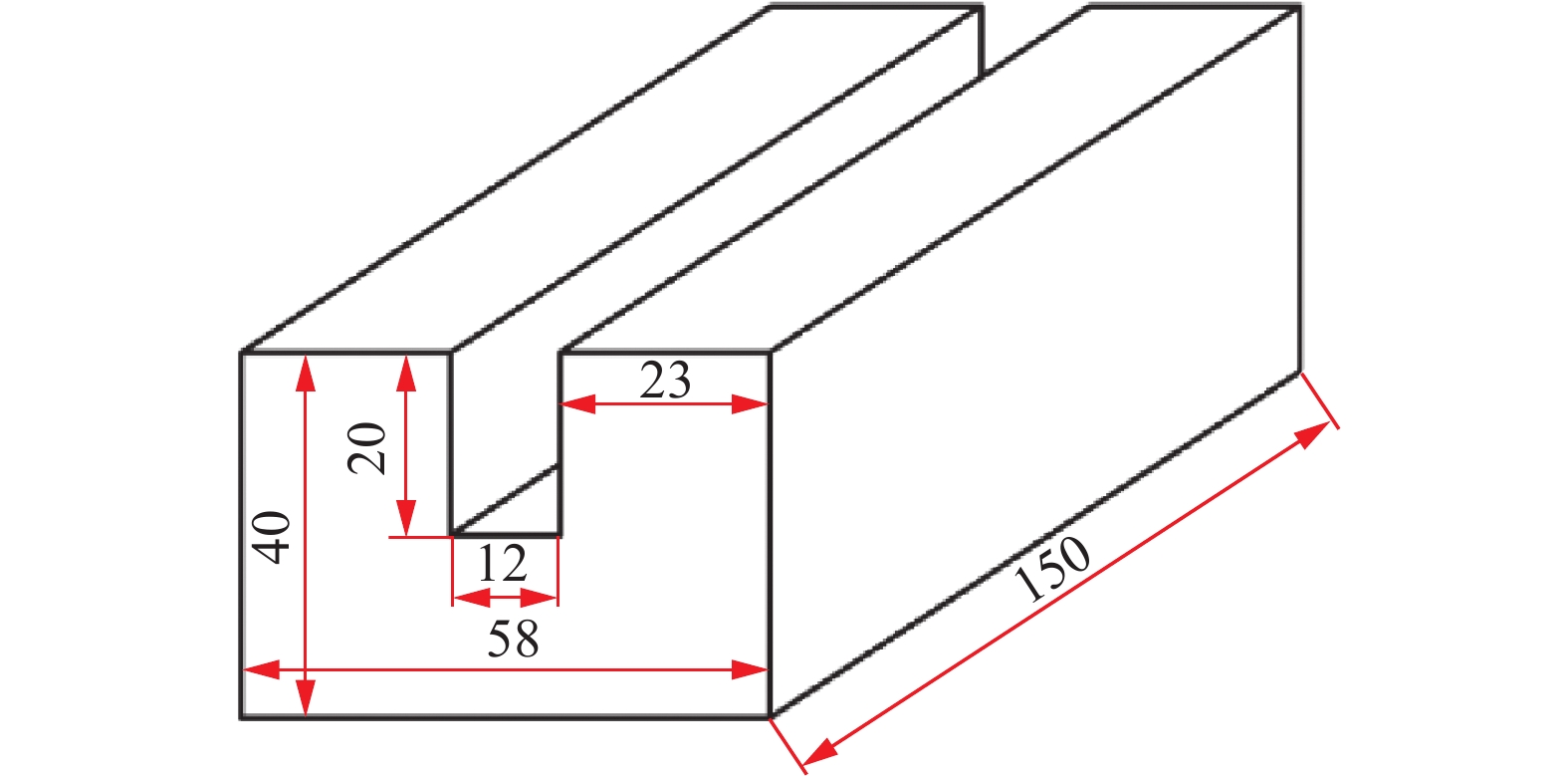
图 3 摇动电弧窄间隙GMA焊电弧形态与结构原理图Figure 3. Schematic diagram of arc shape and structure of SA–NG–GMAW. (a) arc shape under a high-speed camera; (b) diagram of SA–NG–GMAW文中主丝电流为320 A，电弧电压为30 V，焊接速度$ {v}_{0}=240\;{\mathrm{mm/min}} $，摇动频率为4 Hz，摇动角度为66°，侧壁停留时间为60 ms，导电杆弯曲角为8°，辅丝送丝速度为5 m/min。母材为Q370qE，焊丝牌号ER50-6，保护气体为80%Ar+20%CO2的混合气，焊接坡口形式及尺寸如图5所示，间隙为12 mm，深度为20 mm。
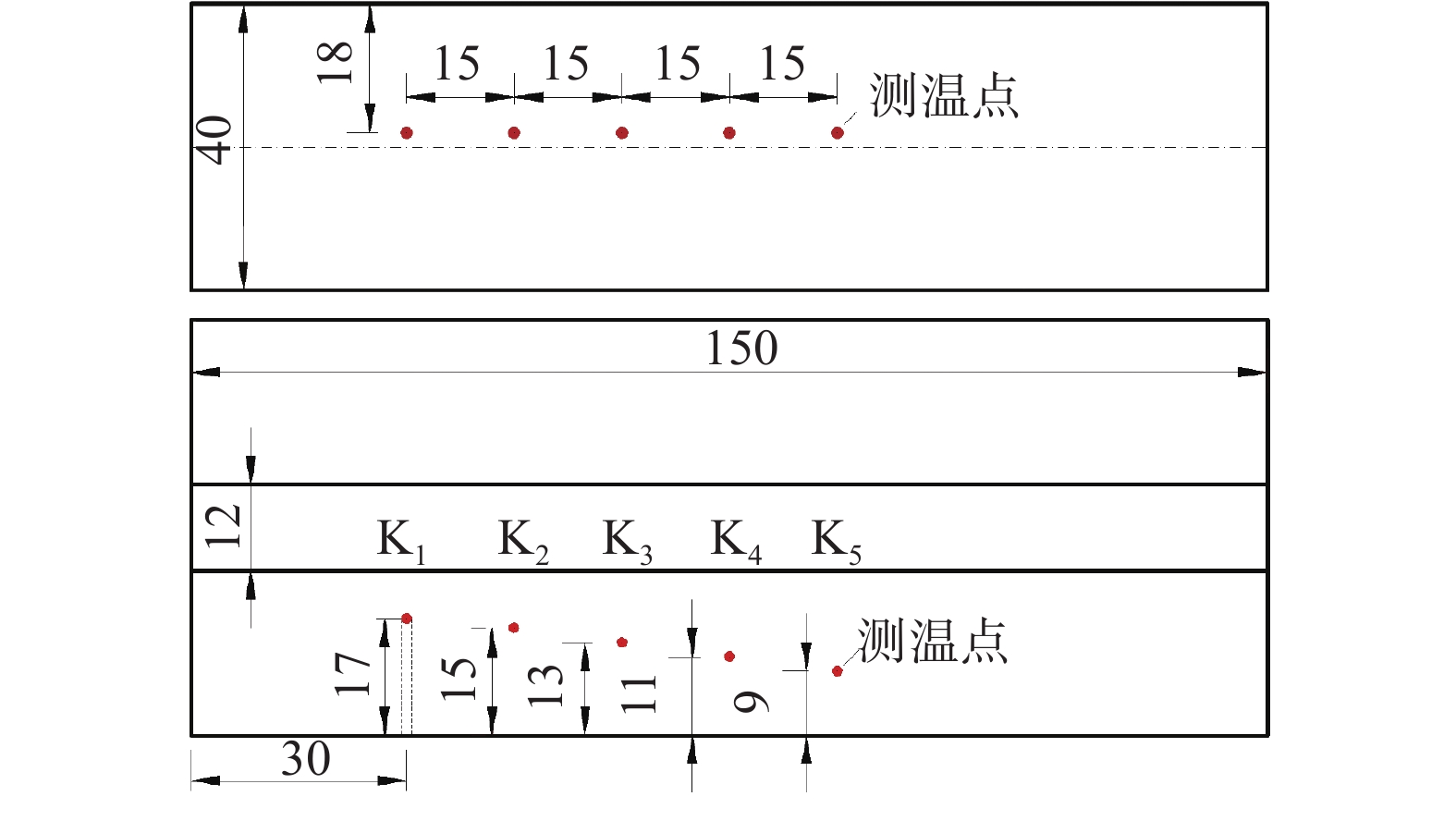
采用热电偶测温技术，测试焊接试件温度分布曲线。设置了5个测温孔，孔底为测温特征点，测温孔具体位置如图6所示。测温采用直径为ϕ1.5 mm的K形铠装热电偶和YOKOGAWA-DX2000无纸记录仪。焊接前，将热电偶预先插入各测温孔中，实时测量该点在焊接过程中的温度变化。试件测温实物如图2所示。
2. 有限元模型的建立
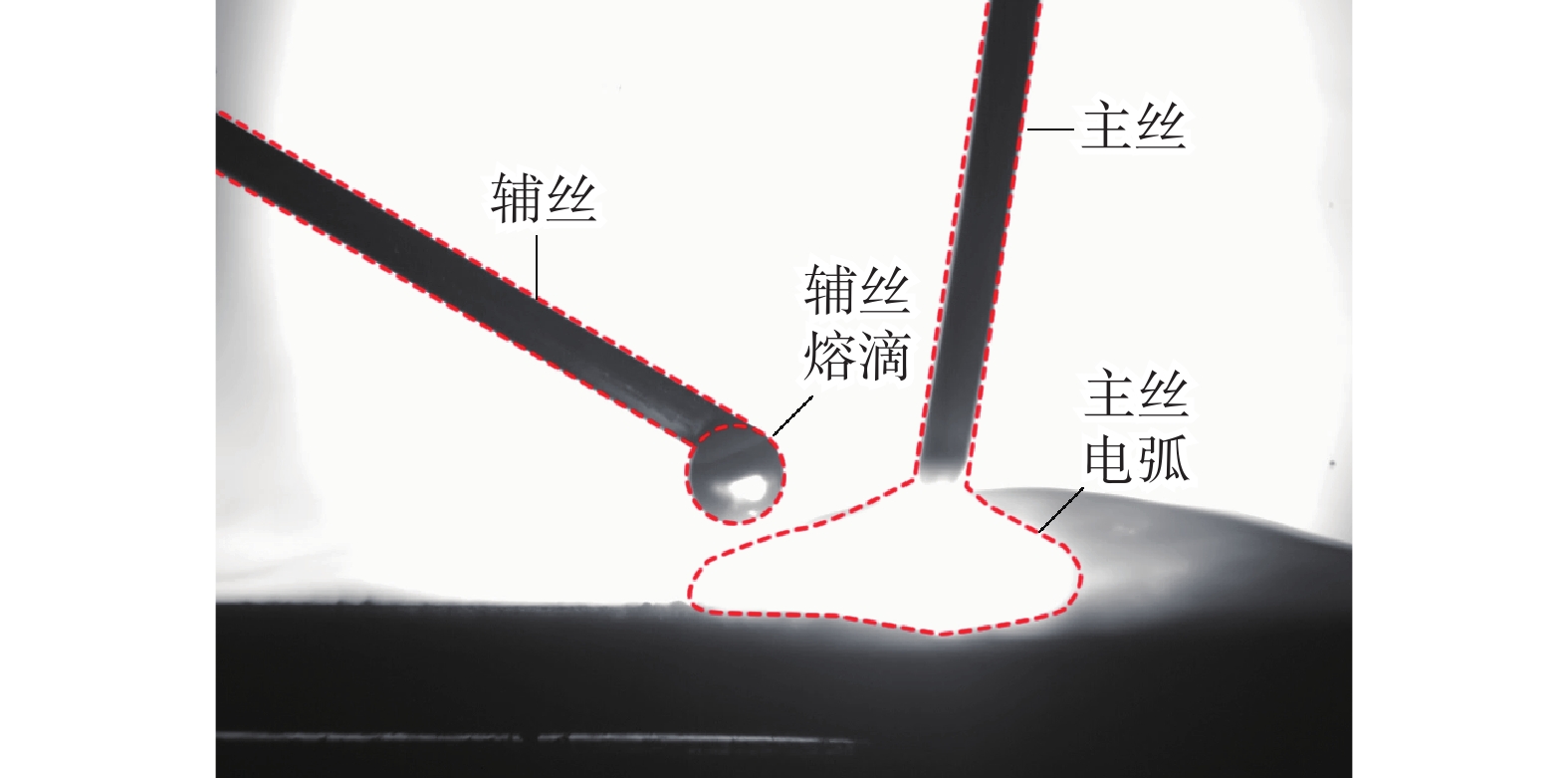
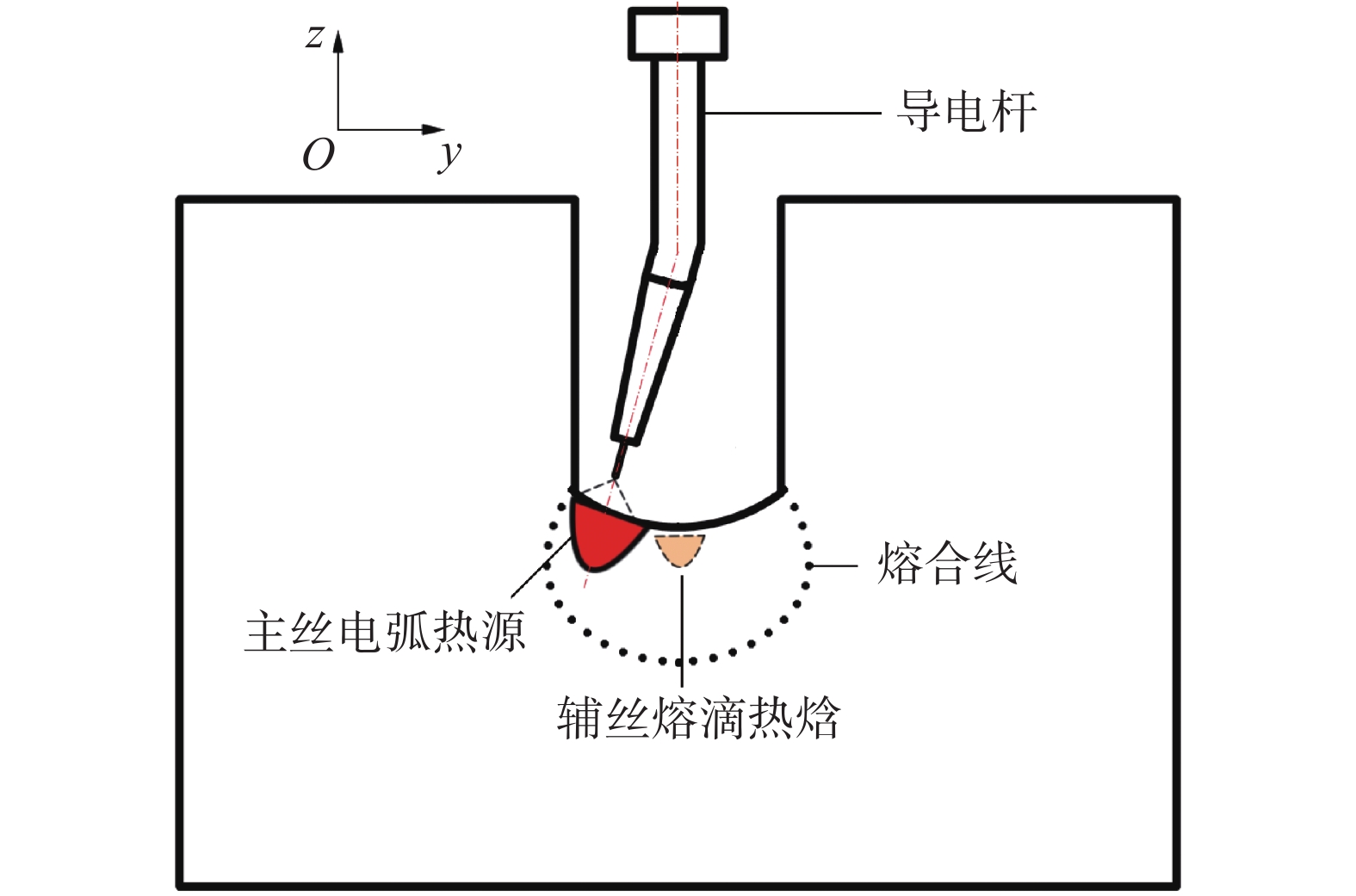
在摇动电弧窄间隙GMA焊过程中，当电弧到达两侧壁时，电弧既加热焊缝，又加热侧壁，因此文中采用双椭球体热源。辅丝位于主丝前方，辅丝与工件不产生电弧，但会吸收主丝电弧部分热量，并以熔滴热焓的方式传递给熔池，如图7所示，因此在计算时，将电弧热源分解成主丝电弧热源和辅丝熔滴热焓，如图8所示。
辅丝与工件之间不产生电弧，也没有电流经过，辅丝熔滴与主丝熔滴之间没有明显的力的相互作用。从前期的高速摄像试验也可以看出，添加辅丝后，主丝熔滴过渡形式变化不明显，但是辅丝会吸收一部分主丝电弧热量，因此主丝熔滴过渡速度有所下降。
2.1 控制方程
传热控制方程为
$$\begin{split}& \rho \left[\frac{\partial H}{\partial t}+u\frac{\partial H}{\partial x}+v\frac{\partial H}{\partial y}+w\frac{\partial H}{\partial {\textit{z}}}\right]=\\&\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial {\textit{z}}}\left(k\frac{\partial T}{\partial {\textit{z}}}\right)+{S}_{{\mathrm{v}}} \end{split} $$ (1) 式中：$ H $是熔滴热焓；$ \rho $是密度；$ k $是热导率；$ t $是时间；$ u $，$ v $和$ w $是$ x $，$ y $，${\textit{z}} $方向上的速度分量；$ {S}_{\mathrm{v}} $是内热源强度。
2.2 主丝电弧热源模型的建立
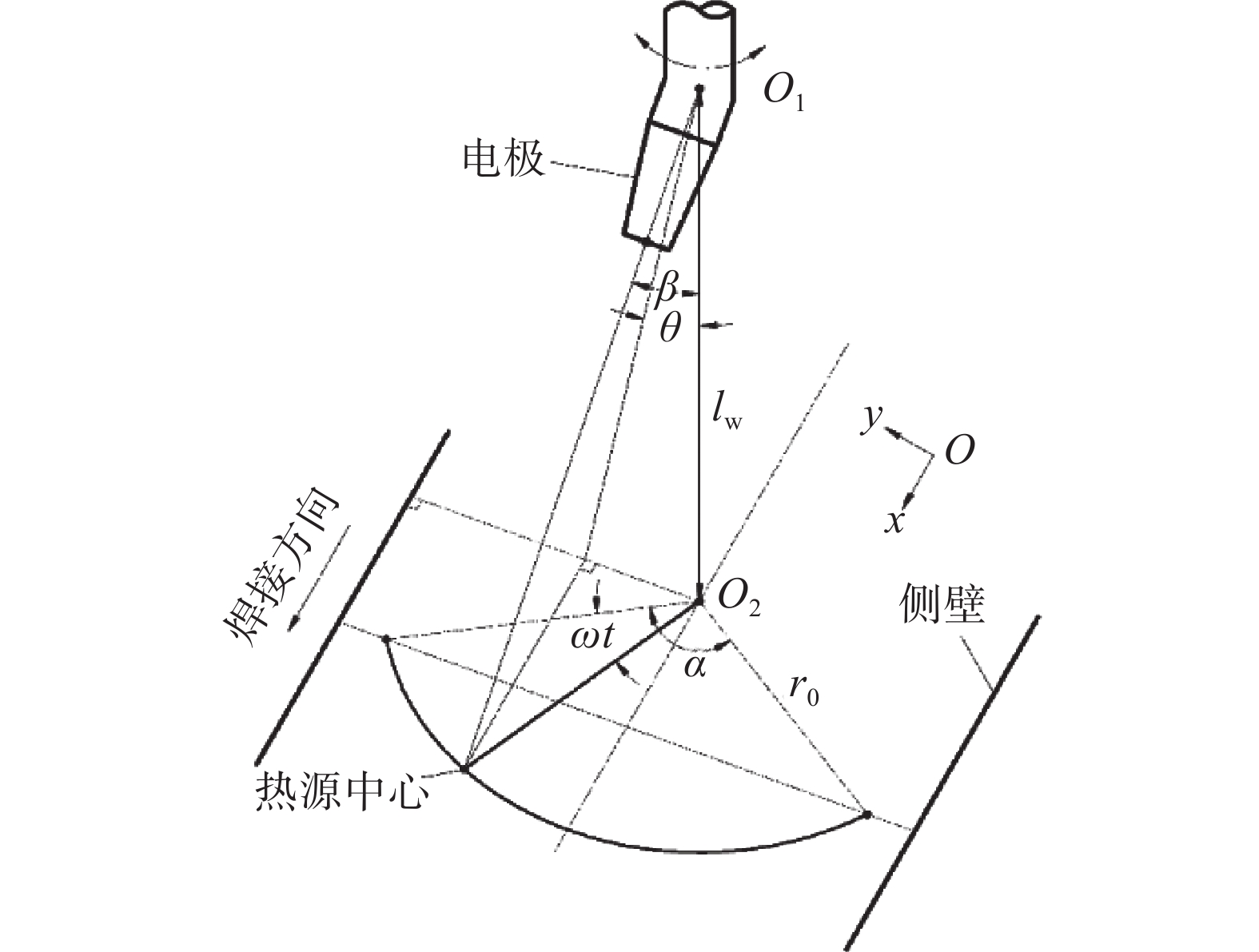
图9给出了电弧摇动角度，t为时间，ω为摇动角速度，ωt为某一时刻电极摇动角度。焊接时，焊丝一方面有沿焊道的直线运动，其速度是v0，另一方面，焊丝绕着焊枪轴线进行往复转动，其速度是vf，焊丝转动过程中，其轨迹为圆弧形，而焊枪在垂直于焊道方向上没有运动，如图4所示。主丝摇动频率f、摇动角度α、摇动半径r0、摇动角速度ω、导电杆弯曲角β、侧壁停留时间tp、焊接速度v0等都会影响电弧轨迹，进而会影响电弧热作用特征。另外，辅丝的加入也会影响温度场分布。
主丝电弧采用双椭球体热源描述电弧热输入，其热源中心$ \left({x}_{1\mathrm{c}},{y}_{1\mathrm{c}},{{\textit{z}}}_{1\mathrm{c}}\right) $与焊接速度$ {v}_{0} $、摇动频率、摇动半径$ {r}_{0} $、摇动角度$ \alpha $等参数有关，即
$$ {x}_{1{\mathrm{c}}}={v}_{0}t+{r}_{0}\mathrm{sin}\left(\frac{{\text{π}} }{2}-\frac{\alpha }{2}+\omega t\right) $$ (2) $$ {y}_{1{\mathrm{c}}}={r}_{0}\mathrm{cos}\left(\frac{{\text{π}} }{2}-\frac{\alpha }{2}+\omega t\right) $$ (3) $$ {{\textit{z}}}_{1\mathrm{c}}={{\textit{z}}}_{0} $$ (4) 2.3 坐标转换
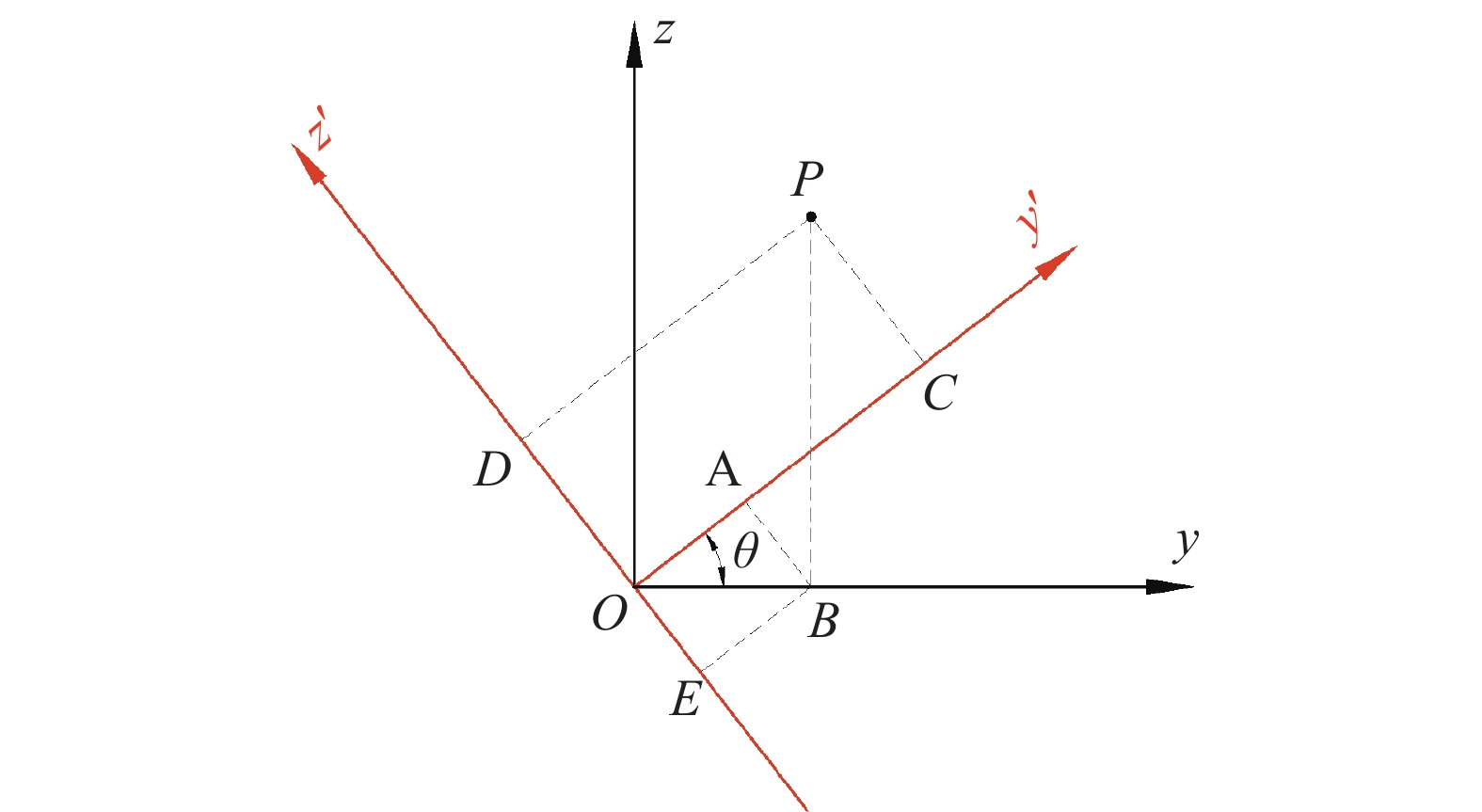
为了便于热源模型的加载，通过坐标转换推算出主丝电弧热源模型摇动后的热流分布函数。图10为坐标系转换示意图。坐标系$ {O}_{xy{\textit{z}}} $逆时针绕x轴旋转角度$ \theta $后形成新坐标系$ {O}_{{x}'{y}'{{\textit{z}}}'} $。原坐标系中的点P坐标为$ \left(x,y,{\textit{z}}\right) $，而其在新坐标系为$ \left({x}{'},{y}{'},{\textit{z}}'\right) $，而当热源中心按式（2）～式（4）表征的移动轨迹移动到某一点$ \left({x}_{{\mathrm{c}}},{y}_{{\mathrm{c}}},{{\textit{z}}}_{{\mathrm{c}}}\right) $时，则存在如下关系，即
$$ {x}'=x-{v}_{0}t-{r}_{0}\mathrm{cos}\left(\frac{{\text{π}} }{2}-\frac{\alpha }{2}+\omega t\right) $$ (5) $$ {y}'=\left[y-{r}_{0}\mathrm{cos}\left(\frac{{\text{π}} }{2}-\frac{\alpha }{2}+\omega t\right)\right]\mathrm{cos}\theta -\left({\textit{z}}-{{\textit{z}}}_{0}\right)\mathrm{sin}\theta $$ (6) $$ {{\textit{z}}}'=y\mathrm{cos}\theta +{\textit{z}}\mathrm{sin}\theta $$ (7) 式（5）～式（7）中转动角度θ在坐标系顺时针转动时取负值。随着主焊丝往复摇动，热源在垂直焊道平面内产生的倾斜角度θ不断变化，当电极由右侧向左侧摇动时为
$$ \theta ={\mathrm{arctan}}\left(\dfrac{{r}_{0}\mathrm{sin}\left(\dfrac{\alpha }{2}-\omega t\right)}{{l}_{{\mathrm{w}}}}\right)=\arctan\left[{\mathrm{tan}}\beta\mathrm{sin}\left(\dfrac{\alpha }{2}-\omega t\right)\right] $$ (8) 式中：当电极由y轴负向向其正向摇动时，θ则取负值。
将式（5）～式（8）代入下述新坐标系下双椭球体热源模型分布函数，则可获得原坐标$ \left(x,y,{\textit{z}}\right) $表示的具有上述热源中心移动轨迹及倾斜角度的热源模型分布函数，即
$$ {q}_{{\mathrm{f}}1}=\frac{12\sqrt{3}{\eta }_{1}IU}{\left({a}_{\mathrm{f}1}+{a}_{\mathrm{r}1}\right){b}_{1}{c}_{1}\mathrm{{\text{π}} }\sqrt{\mathrm{{\text{π}} }}}{\mathrm{exp}}\left(-\frac{3{{x}'}^{2}}{{a}_{{\mathrm{f}}1}^{2}}-\frac{3{{y}'}^{2}}{{b}_{1}}-\frac{3{{{\textit{z}}}'}^{2}}{{c}_{1}}\right) $$ (9) $$ {q}_{{\mathrm{r}}1}=\frac{12\sqrt{3}{\eta }_{1}IU}{\left({a}_{\mathrm{f}1}+{a}_{\mathrm{r}1}\right){b}_{1}{c}_{1}\mathrm{{\text{π}} }\sqrt{\mathrm{{\text{π}} }}}{\mathrm{exp}}\left(-\frac{3{{x}'}^{2}}{{a}_{{\mathrm{r}}1}^{2}}-\frac{3{{y}'}^{2}}{{b}_{1}}-\frac{3{{{\textit{z}}}'}^{2}}{{c}_{1}}\right) $$ (10) 式中：$ {\eta }_{1} $为电弧热效率；$ I $为焊接电流；$ U $为电弧电压；$ {a}_{\mathrm{f}1} $, $ {a}_{\mathrm{r}1} $, b1, c1为热源分布参数。
2.4 辅丝熔滴热焓模型的建立
辅丝不摆动时，辅丝位于主丝前方h的位置，其热源中心$ \left({x}_{2\mathrm{c}},{y}_{2\mathrm{c}},{{\textit{z}}}_{2\mathrm{c}}\right) $为
$$ {x}_{\rm 2c}={v}_{0}t+{r}_{0}\mathrm{sin}\left(\frac{{\text{π}} }{2}-\frac{\alpha }{2}+\omega t\right)+h $$ (11) $$ {y}_{\rm 2c}=0 $$ (12) $$ {{\textit{z}}}_{\rm 2c}={{\textit{z}}}_{0} $$ (13) 辅丝与主丝同步摆动时，辅丝在y方向上为平移运动，其热源中心$ \left({x}_{2\mathrm{c}},{y}_{2\mathrm{c}},{{\textit{z}}}_{2\mathrm{c}}\right) $为
$$ {x}_{2\mathrm{c}}={v}_{0}t+{r}_{0}\mathrm{sin}\left(\frac{\text{π}}{2}-\frac{\alpha }{2}+\omega t\right)+h $$ (14) $$ {y}_{2{\mathrm{c}}}={r}_{0}\mathrm{cos}\left(\frac{\text{π}}{2}-\frac{\alpha }{2}+\omega t\right) $$ (15) $$ {{\textit{z}}}_{2\mathrm{c}}={{\textit{z}}}_{0} $$ (16) 将式（11）～式（13）和式（14）～式（16）分别代入双椭球体热源模型分布函数，得到新的双椭球体热源模型分布函数，即
$$ {q}_{\mathrm{f}2}=\frac{12\sqrt{3}{\eta }_{2}IU}{\left({a}_{\mathrm{f}2}+{a}_{\mathrm{r}2}\right){b}_{2}{c}_{2}{\text{π}}\sqrt{{\text{π}}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{3{{x}_{\rm 2c}}^{2}}{{a}_{{\mathrm{f}}2}^{2}}-\frac{3{{y}_{\rm 2c}}^{2}}{{b}_{2}}-\frac{3{{{\textit{z}}}_{\rm 2c}}^{2}}{{c}_{2}}\right) $$ (17) $$ {q}_{\mathrm{r}2}=\frac{12\sqrt{3}{\eta }_{2}IU}{\left({a}_{\mathrm{f}2}+{a}_{\mathrm{r}2}\right){b}_{2}{c}_{2}{\text{π}}\sqrt{\mathrm{{\text{π}} }}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{3{{x}_{2\mathrm{c}}}^{2}}{{a}_{\mathrm{r}2}^{2}}-\frac{3{{y}_{2\mathrm{c}}}^{2}}{{b}_{2}}-\frac{3{{{\textit{z}}}_{\rm 2c}}^{2}}{{c}_{2}}\right) $$ (18) 式中：$ {\eta }_{2} $为电弧热效率；$ {a}_{\mathrm{f}2} $, $ {a}_{\mathrm{r}2} $, b2, c2为热源分布参数。
2.5 有限元模型
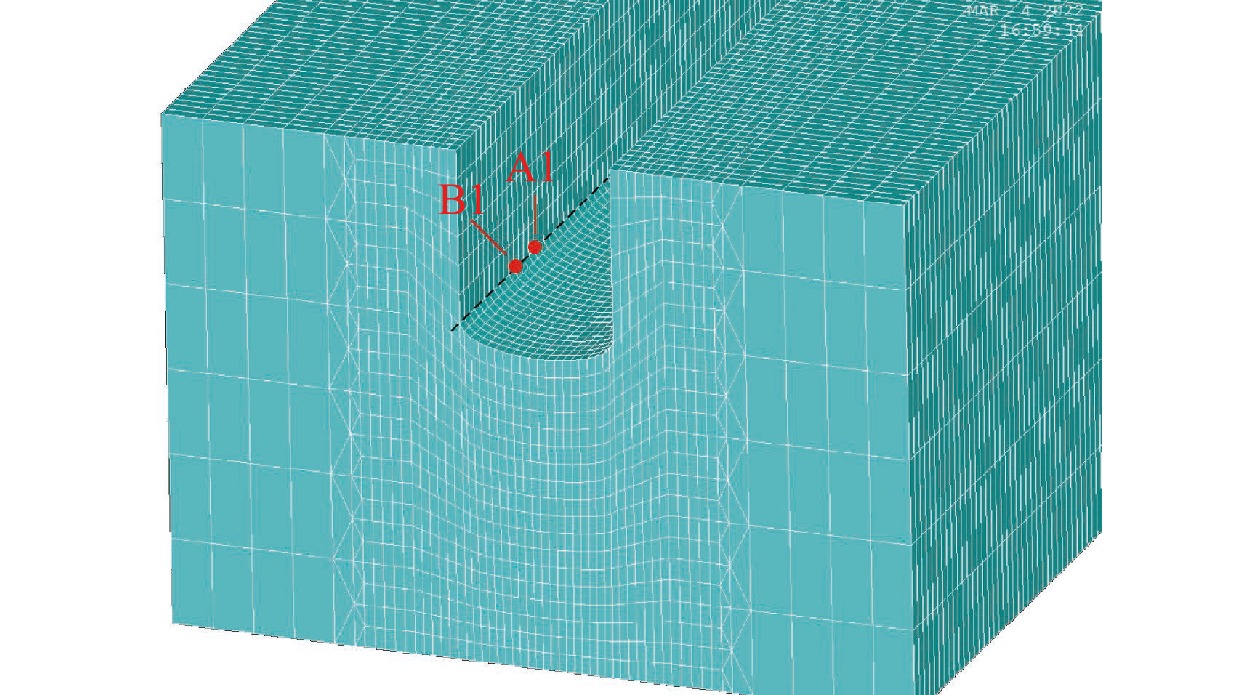
如图11所示，对工件进行建模和网格划分，近缝区网格较密，远离焊缝区域网格较疏。采用“生死”单元法反映填充金属对焊接传热过程的影响，为了考虑焊缝表面形状对热源加载的影响，热源中心始终分布于预先依据试验结果设置的焊缝表面轮廓线上，如图4所示，而热源施加位置如图3(b)所示。
3. 结果与分析
通过ANSYS软件对添加辅丝的摇动电弧窄间隙GMA焊瞬态温度场进行计算。焊件表面考虑对流及辐射散热，环境及初始温度设为20 ℃，熔点取1 500 ℃，性能参数见表1。
表 1 热物理性能参数Table 1. Thermo-physical properties温度
T/℃密度
ρ/(kg·m−3)热导率
λ/(W·m−1·℃−1)比热
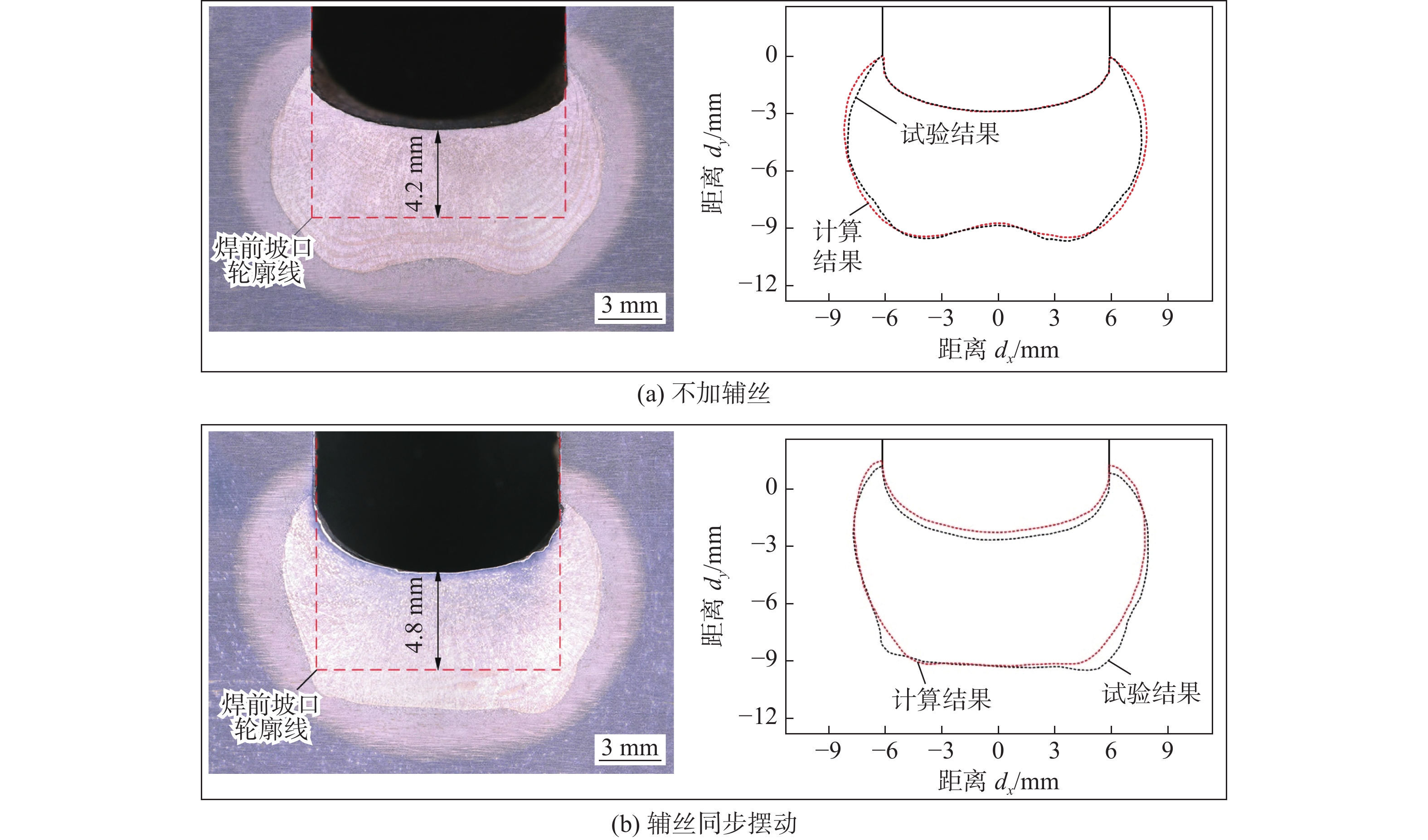
c/(J·kg−1·℃)20 7 800 51.9 450 100 7 740 51.1 499 300 7 700 46.1 565 550 7 610 37.5 705 750 7 550 30.6 1 080 1 000 7 490 29.4 437 1 200 7 400 29.7 400 图12给出了不加辅丝、辅丝同步摆动情况下焊缝横断面试验结果与计算结果，由图可知，2种情况下焊缝横断面形状与试验结果较为接近。不加辅丝情况下，由于主丝电弧在两侧停留时间较长，有明显的“双峰”现象，“双峰”现象的出现会使底部熔深不均匀，影响焊缝质量；辅丝同步摆动情况下，辅丝一直跟随主丝电弧，辅丝吸收了部分主丝电弧的热量，辅丝的熔化量增加，使焊缝高度增加，电弧对焊缝底部影响减弱，因此“双峰”特征不明显。由此可见，辅丝的加入不仅可以提高整体的金属熔敷效率，还能有效地抑制焊缝底部的“双峰”现象。
![]()
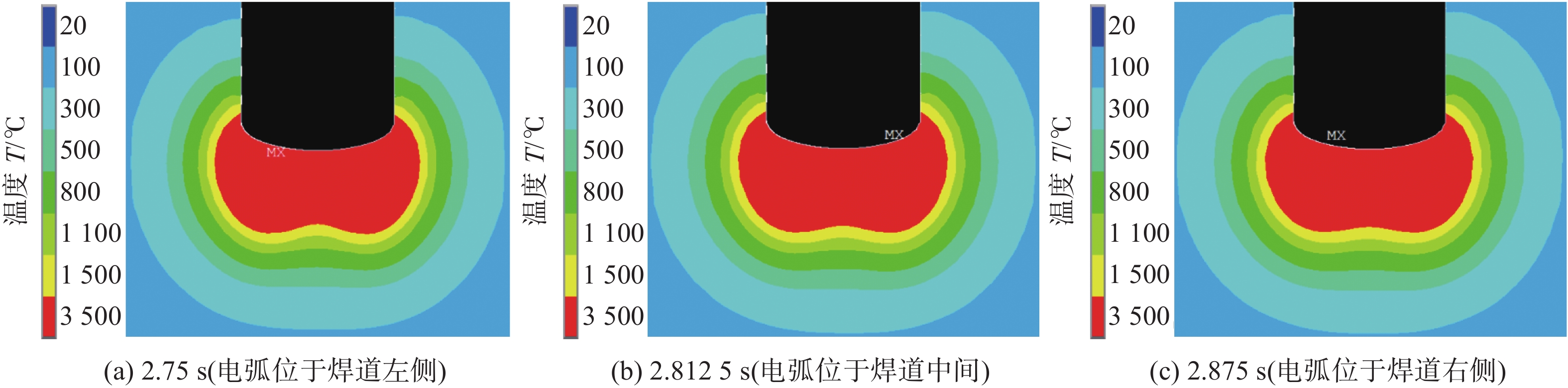
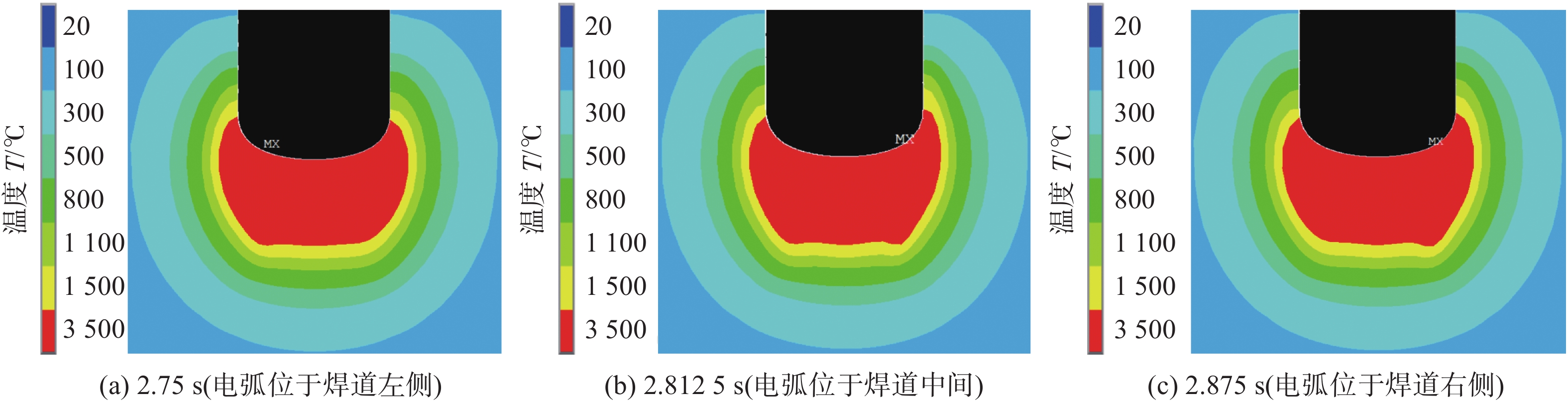
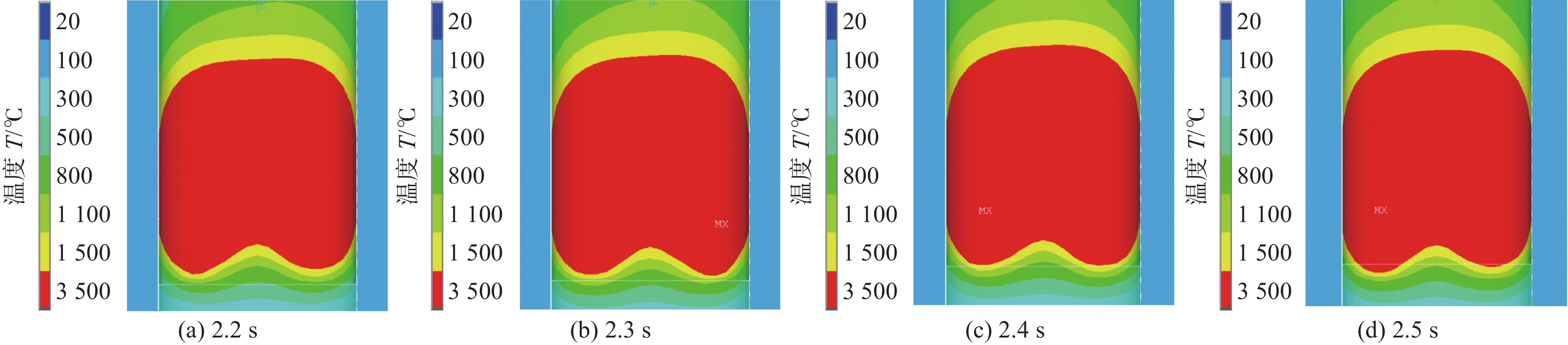
图 12 焊缝横断面试验结果与计算结果的比较Figure 12. Comparison of experimental and calculated weld cross-section. (a) without additional wire; (b) additional wire sync swings图13和图14给出了一个周期内不同时刻焊件横断面温度场的计算结果。可见，在一个周期内，熔池横断面形态保持基本稳定，没有明显变化，这是因为电弧热作用具有延迟性，主丝电弧摇动频率很高，摇动速度很快，来不及散热，主丝就又在下个周期摇动到该位置，使主丝电弧在整个坡口范围内加热较为均匀。
![]()
图 13 不同时刻焊件横断面温度场计算结果（不加辅丝）Figure 13. Calculated temperature fields at the cross-section of the workpiece at different times (without additional wire). (a) 2.75 s (left side of the weld bead); (b)2.8125 s (in the middle of the weld bead); (c) 2.875 s (right side of weld bead)![]()
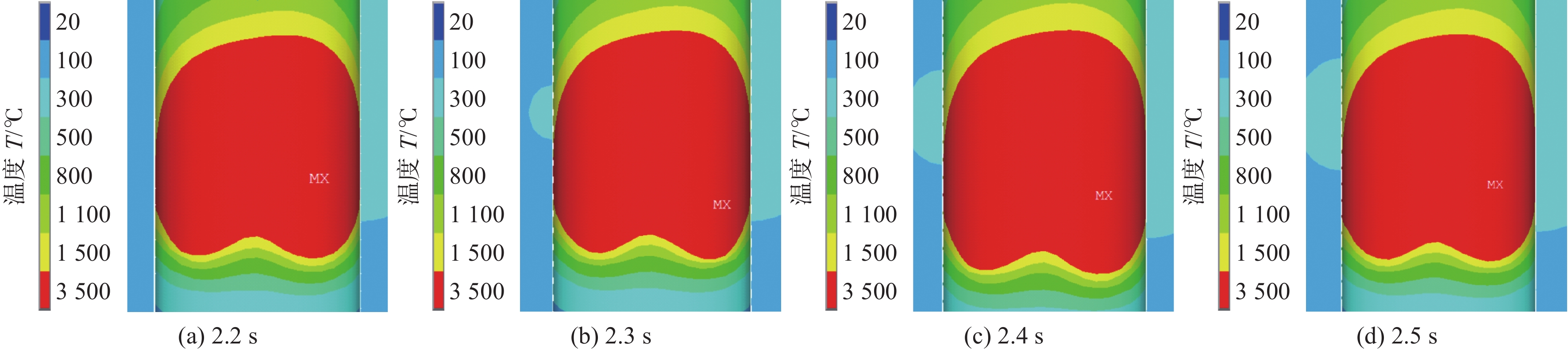
图 14 不同时刻焊件横断面温度场计算结果（辅丝同步摆动）Figure 14. Calculated temperature fields at the cross-section of the workpiece at different times (additional wire sync swings). (a) 2.75 s (left side of the weld bead); (b)2.8125 s (in the middle of the weld bead); (c) 2.875 s (right side of weld bead)图15和图16是焊接开始熔池的形态变化。如图15(a)所示，在t=0.025 s时，在右侧形成熔池，但由于母材温度较低，熔池尺寸较小；当电弧向左侧移动，熔池尺寸增加，如图15(b)所示。由于主丝电弧摇动速度较快，且在左右两侧停留时间较长，导致首先在两侧形成熔池。母材温度不断升高，左右两侧的熔池尺寸不断扩大，如图15(c)所示。随着时间的推移，熔池尺寸进一步扩大，直至横跨整个焊道，如图15(d)所示。图16是辅丝同步摆动情况下熔池形态变化图，辅丝的加入，使主丝电弧一部分热量用于熔化辅丝，因此在相同时间时，左右两侧的熔池尺寸较不加辅丝时要小，如图16(a)和图16(b)所示。随着时间的推移，辅丝熔滴进入焊道中间，同时将熔滴热焓传递给焊道中间，使整个焊道的热量分布更加均匀，如图16(c)和图16(d)所示。
![]()
图 15 稳定前焊件表面温度场计算结果（不加辅丝）Figure 15. Evolution of temperature fields at the top surface of workpiece before reaching quasi-steady state (without additional wire). (a) 0.025 s; (b) 0.15 s; (c) 0.6 s; (d) 1.0 s![]()
图 16 稳定前焊件表面温度场计算结果（辅丝同步摆动）Figure 16. Evolution of temperature fields at the top surface of workpiece before reaching quasi-steady state (additional wire sync swings). (a) 0.025 s; (b) 0.15 s; (c) 0.6 s; (d) 1.0 s图17和图18给出了焊接稳定后一个周期内，上表面温度场的计算结果，可见熔池表面形状变化不大。主丝摇动频率为4 Hz，一个周期0.25 s，而左右两侧停留时间都是0.06 s，停留时间较长，这使得熔池在左右两侧沿焊接方向有所凸前。如图13、图14和图17、图18所示，电弧摇动对熔池动态行为影响不大，这是因为文中采用的焊接电流较大，熔池也较大，而焊件间隙较窄，散热不及时，同时摇动频率又很高。
![]()
图 17 稳定后焊件表面温度场计算结果（不加辅丝）Figure 17. Calculated temperature fields at the top surface of the workpiece at different times (without additional wire). (a) 2.2 s; (b) 2.3 s; (c) 2.4 s; (d) 2.5 s![]()
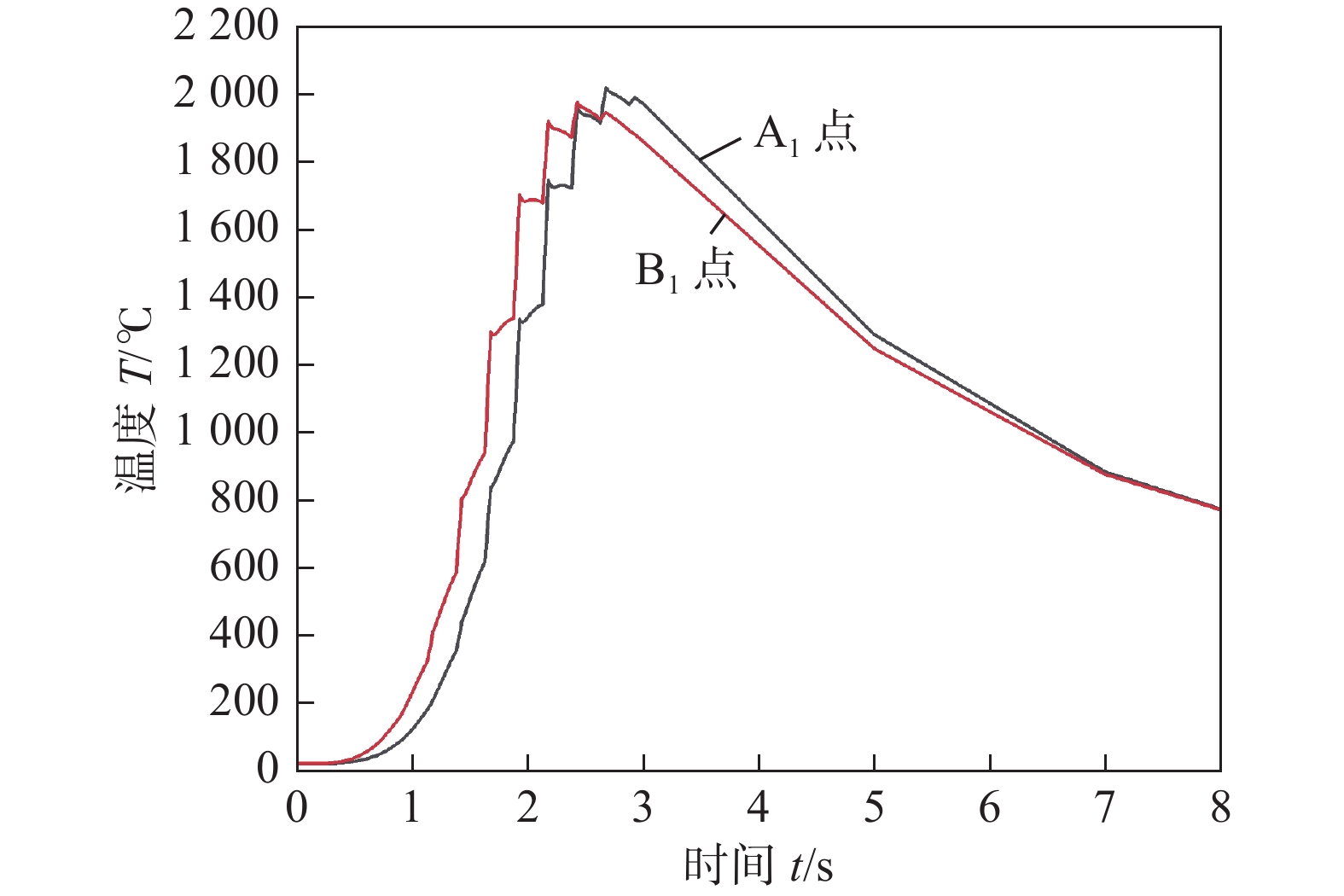
图 18 稳定后焊件表面温度场计算结果（辅丝同步摆动）Figure 18. Calculated temperature fields at the top surface of the workpiece at different times (additional wire sync swings). (a) 2.2 s; (b) 2.3 s; (c) 2.4 s; (d) 2.5 s图19为不加辅丝情况下，焊趾处A1点和B1点（如图11所示，A1点与B1点x方向相差1 mm）热循环曲线的计算结果。由于受主丝电弧摇动特性及焊道几何特征的影响，曲线均存在5个峰值，相邻两峰值之间的时间间隔为一个摇动周期，即0.25 s；A1与B1都位于焊道左侧焊趾处，但两点在x方向位置不同，导致主丝电弧在左侧停留时，对两点的加热时间有所不同，因此两点的最大峰值温度略有不同。当主丝电弧到达该点前3个周期时，加热阶段出现较小峰值；当一个周期过后，主丝电弧移至该点时，其温度达到最大值；而一个周期后，冷却阶段再次出现峰值，是由于一个周期内电弧前行距离较短，主丝电弧移至该点侧壁时，再次使其温度升高。随着主丝电弧热源离该点距离的持续增加，再无峰值出现。A1与B1两点的冷却时间$ {t}_{8/5} $相近，分别为3.74 s和3.91 s。
![]()
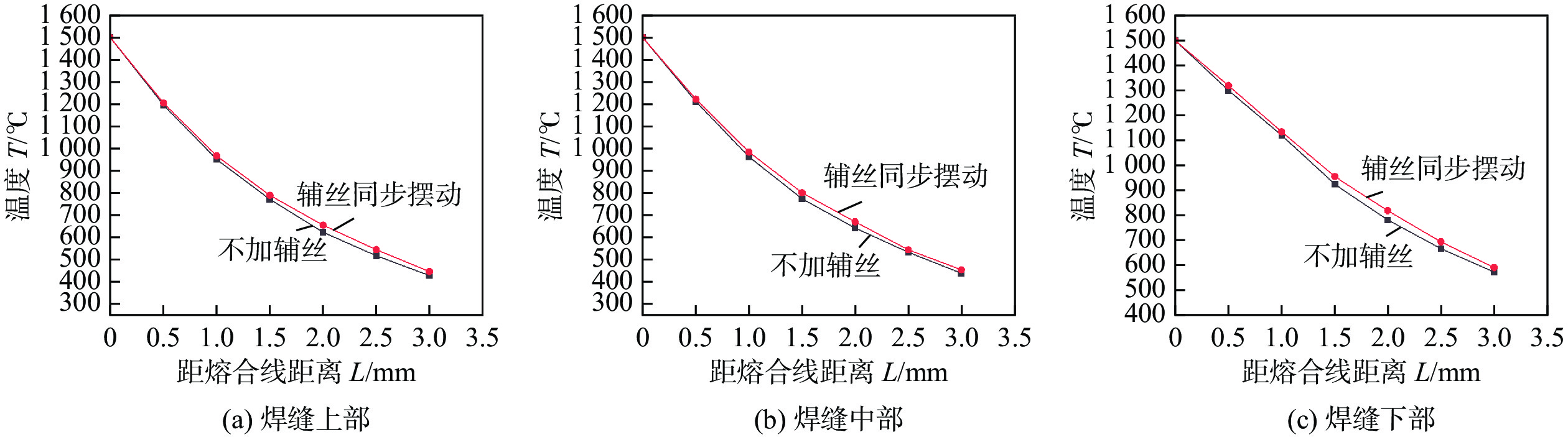
图 19 A1点和B1点热循环曲线计算结果（不加辅丝）Figure 19. Calculation of the thermal cycling at points A1 and B1 (without additional wire)图20给出了3种情况下，焊缝上部、焊缝中部、焊缝下部距离熔合线不同位置各点的温度（t=2.875 s），可以看出，不加辅丝时温度下降较快，温度梯度较大，其热影响区宽度也较窄；辅丝同步摆动时下降较慢，温度梯度较小，其热影响区宽度也较宽。但是两者之间的差距很小。由此可以看出，热辅丝的加入，在有效地提高熔覆效率情况下，并不会明显地增加热影响区宽度。
![]()
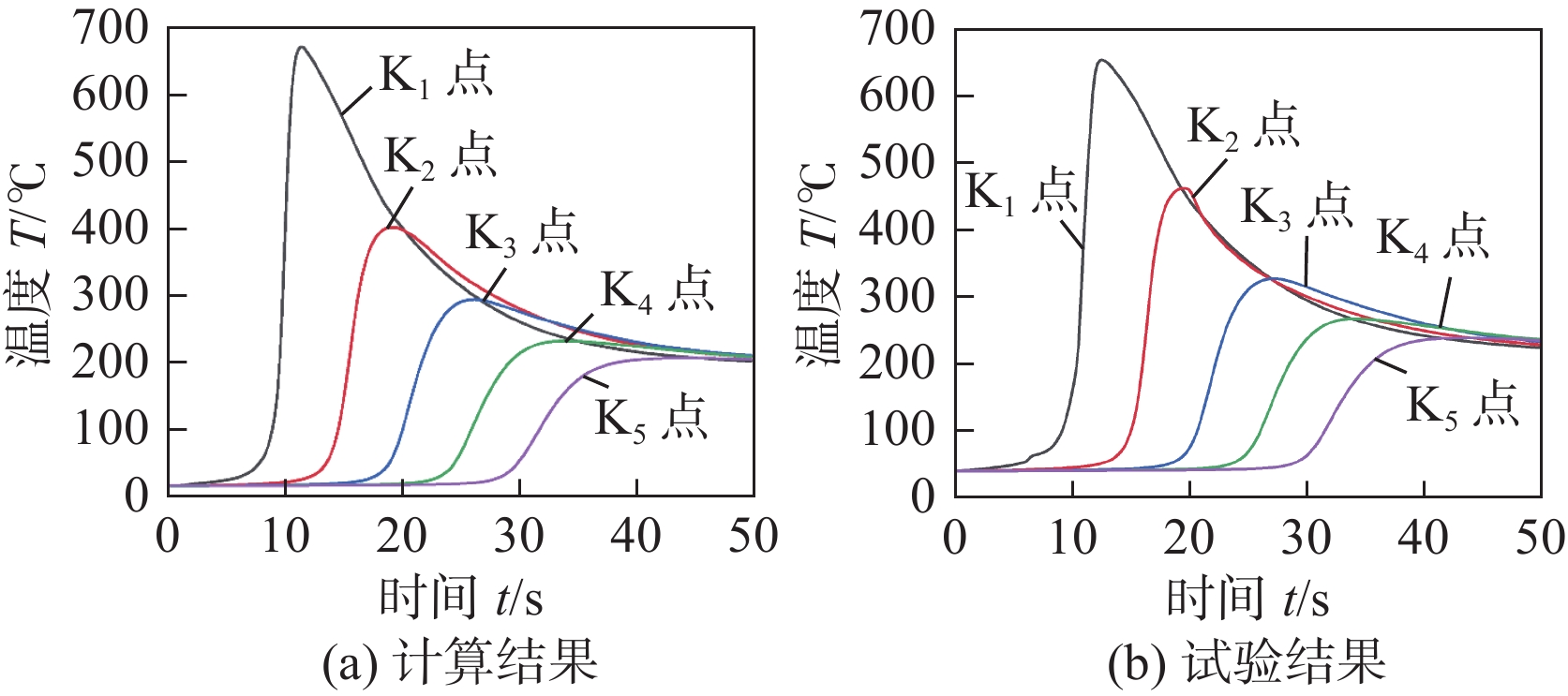
图 20 距熔合线不同位置各点温度(t=2.875 s)Figure 20. Temperatures at different points from the fusion line (t= 2.875 s). (a) upper part of weld; (b) middle part of weld; (c) lower part of weld图21为不加辅丝情况下测温特征点的热循环曲线计算结果和试验结果对比，具体测温特征点位置及分布如图6所示。可以看出，计算结果与试验结果较为接近，进一步证明了文中模型的准确性。另外，由于测温特征点距离主丝电弧较远，受主丝电弧左右摇动的影响较小，因此，5个测温特征点热循环曲线均只出现一个温度峰值，与实测结果一致。
![]()
图 21 测温特征点热循环曲线计算结果与试验结果对比（不加辅丝）Figure 21. Comparison of the calculated and experimental thermal cycles (without additional wire). (a) calculation results; (b) experimental results4. 结论
（1）文中建立了添加辅丝的摇动电弧窄间隙GMA焊瞬态温度场数值分析模型，计算结果与试验结果较为接近，模型能够准确地反映温度场的特性。
（2）在试验条件下，焊接相对稳定后，在一个周期内，熔池形态变化不大。不加辅丝时，焊缝横断面底部有明显“双峰”现象，辅丝同步摆动时，“双峰”特征减弱，因此辅丝的加入能够有效地抑制“双峰”现象。
（3）不加辅丝时热影响区宽度较窄，辅丝同步摆动时较宽，但是差距很小，热辅丝的加入，在有效地提高熔覆效率情况下，并不会明显地增加热影响区宽度。
-
![]()
图 1 添加辅丝的摇动电弧窄间隙GMA焊系统原理示意图
Figure 1. Diagram of the SA–NG–GMAW system with additional wire
![]()
图 3 摇动电弧窄间隙GMA焊电弧形态与结构原理图
Figure 3. Schematic diagram of arc shape and structure of SA–NG–GMAW. (a) arc shape under a high-speed camera; (b) diagram of SA–NG–GMAW
![]()
图 12 焊缝横断面试验结果与计算结果的比较
Figure 12. Comparison of experimental and calculated weld cross-section. (a) without additional wire; (b) additional wire sync swings
![]()
图 13 不同时刻焊件横断面温度场计算结果（不加辅丝）
Figure 13. Calculated temperature fields at the cross-section of the workpiece at different times (without additional wire). (a) 2.75 s (left side of the weld bead); (b)
2.8125 s (in the middle of the weld bead); (c) 2.875 s (right side of weld bead)![]()
图 14 不同时刻焊件横断面温度场计算结果（辅丝同步摆动）
Figure 14. Calculated temperature fields at the cross-section of the workpiece at different times (additional wire sync swings). (a) 2.75 s (left side of the weld bead); (b)
2.8125 s (in the middle of the weld bead); (c) 2.875 s (right side of weld bead)![]()
图 15 稳定前焊件表面温度场计算结果（不加辅丝）
Figure 15. Evolution of temperature fields at the top surface of workpiece before reaching quasi-steady state (without additional wire). (a) 0.025 s; (b) 0.15 s; (c) 0.6 s; (d) 1.0 s
![]()
图 16 稳定前焊件表面温度场计算结果（辅丝同步摆动）
Figure 16. Evolution of temperature fields at the top surface of workpiece before reaching quasi-steady state (additional wire sync swings). (a) 0.025 s; (b) 0.15 s; (c) 0.6 s; (d) 1.0 s
![]()
图 17 稳定后焊件表面温度场计算结果（不加辅丝）
Figure 17. Calculated temperature fields at the top surface of the workpiece at different times (without additional wire). (a) 2.2 s; (b) 2.3 s; (c) 2.4 s; (d) 2.5 s
![]()
图 18 稳定后焊件表面温度场计算结果（辅丝同步摆动）
Figure 18. Calculated temperature fields at the top surface of the workpiece at different times (additional wire sync swings). (a) 2.2 s; (b) 2.3 s; (c) 2.4 s; (d) 2.5 s
![]()
图 19 A1点和B1点热循环曲线计算结果（不加辅丝）
Figure 19. Calculation of the thermal cycling at points A1 and B1 (without additional wire)
![]()
图 20 距熔合线不同位置各点温度(t=2.875 s)
Figure 20. Temperatures at different points from the fusion line (t= 2.875 s). (a) upper part of weld; (b) middle part of weld; (c) lower part of weld
![]()
图 21 测温特征点热循环曲线计算结果与试验结果对比（不加辅丝）
Figure 21. Comparison of the calculated and experimental thermal cycles (without additional wire). (a) calculation results; (b) experimental results
表 1 热物理性能参数
Table 1 Thermo-physical properties
温度
T/℃密度
ρ/(kg·m−3)热导率
λ/(W·m−1·℃−1)比热
c/(J·kg−1·℃)20 7 800 51.9 450 100 7 740 51.1 499 300 7 700 46.1 565 550 7 610 37.5 705 750 7 550 30.6 1 080 1 000 7 490 29.4 437 1 200 7 400 29.7 400 
下载: 导出CSV
-
[1] Wang J Y, Zhu J, Fu P, et al. A swing arc system for narrow gap GMA welding[J]. ISIJ International, 2012, 52(1): 110 − 114. doi: 10.2355/isijinternational.52.110
[2] Wang J Y, Ren Y S, Yang F, et al. Novel rotation arc system for narrow gap MAG welding[J]. Science and Technology of Welding and Joining, 2007, 12(6): 505 − 507. doi: 10.1179/174329307X213756
[3] Cai Y X, Lin B S, Fan L C, et al. Molten pool behaviour and weld forming mechanism of tandem narrow gap vertical GMAW[J]. Science and Technology of Welding and Joining, 2016, 21(2): 124 − 130. doi: 10.1179/1362171815Y.0000000073
[4] Xu H W, Lin B S, Fan L C, et al. Statistical modelling of weld bead geometry in oscillating arc narrow gap all-position GMA welding[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72(9-12): 1705 − 1716. doi: 10.1007/s00170-014-5799-2
[5] Xu G X, Wang J Y, Li P F, et al. Numerical analysis of heat transfer and fluid flow in swing arc narrow gap GMA welding[J]. Journal of Materials Processing Technology, 2017, 252: 260 − 269.
[6] Wang J Y, Zhu J, Zhang C, et al. Effect of arc swing parameters on narrow gap vertical GMA weld formation[J]. ISIJ International, 2016, 56(5): 844 − 850. doi: 10.2355/isijinternational.ISIJINT-2015-660
[7] Zhu J, Wang J Y, Su N, et al. An infrared visual sensing detection approach for swing arc narrow gap weld deviation[J]. Journal of Materials Processing Technology, 2016, 243: 258 − 268.
[8] Zhou J L, Shu F Y, Zhao H Y, et al. Microstructure and mechanical properties of heat affected zone in multi-pass GMA welded Al-Zn-Mg-Cu alloy[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(11): 2273 − 2280. doi: 10.1016/S1003-6326(19)65133-2
[9] 黄健康, 孙天亮, 樊丁, 等. TIG焊熔池表面流动行为的研究[J]. 机械工程学报, 2016, 52(18): 31 − 37. Huang Jiankang, Sun Tianliang, Fan Ding, et al. Study on the surface flow behavior of TIG weld pool[J]. Journal of Mechanical Engineering, 2016, 52(18): 31 − 37.
[10] Gao X S, Wu C S, Goecke S F, et al. Numerical simulation of temperature field, fluid flow and weld bead formation in oscillating single mode laser-GMA hybrid welding[J]. Journal of Materials Processing Technology, 2016, 242: 147 − 159.
[11] Serizawa H, Nakamura S, Kanbe K, et al. Numerical analysis of deformation in multi-pass circumferential TIG welding with narrow gap[J]. Weld in the World, 2013, 57(5): 615 − 623. doi: 10.1007/s40194-013-0059-x
[12] 胥国祥, 潘海潮, 王加友. 摇动电弧窄间隙GMAW焊温度场数值分析模型[J]. 焊接学报, 2017, 38(10): 55 − 60. Xu Guoxiang, Pan Haichao, Wang Jiayou. Numerical analysis model of temperature field in swing-arc narrow gap GMAW[J]. Transactions of the China Welding Institution, 2017, 38(10): 55 − 60.
计量
- 文章访问数: 97
- HTML全文浏览量: 21
- PDF下载量: 15
